| 设D是正△P1P2P3及其内部的点构成的集合，点P0是△P1P2P3的中心．若集合S={P|P∈D，|PP0|≤|PPi|，i=1，2，3}，则集合S表示的平面区域是 |
A．三角形区域
B．四边形区域
C．五边形区域
D．六边形区域 |
相关习题
科目：高中数学
来源：
题型：
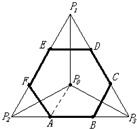
8、设D是正△P
1P
2P
3及其内部的点构成的集合，点P
0是△P
1P
2P
3的中心，若集合S={P|P∈D，|PP
0|≤|PP
i|，i=1，2，3}，则集合S表示的平面区域是（ ）
查看答案和解析>>
科目：高中数学
来源：
题型：
8、设D是正△P
1P
2P
3及其内部的点构成的集合，点P
0是△P
1P
2P
3的中心．若集合S={P|P∈D，|PP
0|≤|PP
i|，i=1，2，3}，则集合S表示的平面区域是
六边形区域
．
查看答案和解析>>
科目：高中数学
来源：
题型：单选题
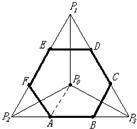设D是正△P1P2P3及其内部的点构成的集合，点P0是△P1P2P3的中心，若集合S={P|P∈D，|PP0|≤|PPi|，i=1，2，3}，则集合S表示的平面区域是
- A.
三角形区域
- B.
四边形区域
- C.
五边形区域
- D.
六边形区域
查看答案和解析>>
科目：高中数学
来源：北京
题型：单选题
设D是正△P
1P
2P
3及其内部的点构成的集合，点P
0是△P
1P
2P
3的中心，若集合S={P|P∈D，|PP
0|≤|PP
i|，i=1，2，3}，则集合S表示的平面区域是（ ）
| A．三角形区域 | B．四边形区域 | C．五边形区域 | D．六边形区域 |
查看答案和解析>>
科目：高中数学
来源：2010-2011学年江西省宜春市樟树中学高二（上）第四次月考数学试卷（文科）（解析版）
题型：选择题
设D是正△P
1P
2P
3及其内部的点构成的集合，点P
是△P
1P
2P
3的中心，若集合S={P|P∈D，|PP
|≤|PP
i|，i=1，2，3}，则集合S表示的平面区域是（ ）
A．三角形区域
B．四边形区域
C．五边形区域
D．六边形区域
查看答案和解析>>
科目：高中数学
来源：2010-2011学年江西省宜春市樟树中学高二（上）第四次月考数学试卷（理科）（解析版）
题型：选择题
设D是正△P
1P
2P
3及其内部的点构成的集合，点P
是△P
1P
2P
3的中心，若集合S={P|P∈D，|PP
|≤|PP
i|，i=1，2，3}，则集合S表示的平面区域是（ ）
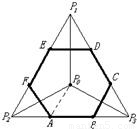
A．三角形区域
B．四边形区域
C．五边形区域
D．六边形区域
查看答案和解析>>
科目：高中数学
来源：2009-2010学年湖北省武汉六中高一（下）第五次月考数学试卷（解析版）
题型：选择题
设D是正△P
1P
2P
3及其内部的点构成的集合，点P
是△P
1P
2P
3的中心，若集合S={P|P∈D，|PP
|≤|PP
i|，i=1，2，3}，则集合S表示的平面区域是（ ）
A．三角形区域
B．四边形区域
C．五边形区域
D．六边形区域
查看答案和解析>>
科目：高中数学
来源：2010-2011学年江苏省盐城市建湖外国语学校高三（上）期末数学试卷（解析版）
题型：选择题
设D是正△P
1P
2P
3及其内部的点构成的集合，点P
是△P
1P
2P
3的中心，若集合S={P|P∈D，|PP
|≤|PP
i|，i=1，2，3}，则集合S表示的平面区域是（ ）
A．三角形区域
B．四边形区域
C．五边形区域
D．六边形区域
查看答案和解析>>
科目：高中数学
来源：《第2章 平面向量》2010年单元测试卷（7）（解析版）
题型：选择题
设D是正△P
1P
2P
3及其内部的点构成的集合，点P
是△P
1P
2P
3的中心，若集合S={P|P∈D，|PP
|≤|PP
i|，i=1，2，3}，则集合S表示的平面区域是（ ）
A．三角形区域
B．四边形区域
C．五边形区域
D．六边形区域
查看答案和解析>>
科目：高中数学
来源：2011年高三数学（文科）一轮复习讲义：4.1 平面向量的概念及线性运算（解析版）
题型：解答题
设D是正△P1P2P3及其内部的点构成的集合，点P是△P1P2P3的中心．若集合S={P|P∈D，|PP|≤|PPi|，i=1，2，3}，则集合S表示的平面区域是 ．
查看答案和解析>>
