函数 （x∈R）的最小值等于 |
A．-3
B．-2
C．-1
D．- |
相关习题
科目：高中数学
来源：高考真题
题型：单选题
函数
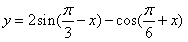
（x∈R）的最小值等于
A．-3
B．-2
C．-1
D．-
查看答案和解析>>
科目：高中数学
来源：2012-2013学年上海市十二校高三（上）12月联考数学试卷（理科）（解析版）
题型：解答题
已知
（a∈R）的图象关于坐标原点对称
（1）求a的值，并求出函数F（x）=f（x）+2
x-
-1的零点；
（2）若函数
在[0，1]内存在零点，求实数b的取值范围
（3）设
，若不等式f
-1（x）≤g（x）在
上恒成立，求满足条件的最小整数k的值．
查看答案和解析>>
科目：高中数学
来源：贵州
题型：单选题
函数
y=2sin(-x)-cos(+x)(x∈R)的最小值等于（ ）
查看答案和解析>>
科目：高中数学
来源：
题型：
已知
f(x)=（a∈R）的图象关于坐标原点对称
（1）求a的值，并求出函数F（x）=f（x）+2
x-
-1的零点；
（2）若函数
h(x)=f(x)+2x-在[0，1]内存在零点，求实数b的取值范围
（3）设
g(x)=log4，若不等式f
-1（x）≤g（x）在
x∈[，]上恒成立，求满足条件的最小整数k的值．
查看答案和解析>>
科目：高中数学
来源：
题型：
把函数f（x）=sin
2x-2sinxcosx+3cos
2x（x∈R）的图象按向量
=(m，0)(m＞0)平移，所得函数y=g（x）的图象关于直线
x=π对称．
（1）设有不等的实数x
1、x
2∈（0，π），且f（x
1）=f（x
2）=1，求x
1+x
2的值；
（2）求m的最小值；
（3）当m取最小值时，求函数y=g（x）的单调递增区间．
查看答案和解析>>
科目：高中数学
来源：不详
题型：解答题
把函数f（x）=sin
2x-2sinxcosx+3cos
2x（x∈R）的图象按向量
=(m，0)(m＞0)平移，所得函数y=g（x）的图象关于直线
x=π对称．
（1）设有不等的实数x
1、x
2∈（0，π），且f（x
1）=f（x
2）=1，求x
1+x
2的值；
（2）求m的最小值；
（3）当m取最小值时，求函数y=g（x）的单调递增区间．
查看答案和解析>>
科目：高中数学
来源：2011-2012学年江苏省南通市启东中学高一（上）期中数学试卷（解析版）
题型：解答题
设函数f（x）=ax2+bx+1，a＞0，b∈R 的最小值为-a，f（x）=0两个实根为x1、x2．
（1）求x1-x2的值；
（2）若关于x的不等式f（x）＜0解集为A，函数f（x）+2x在A上不存在最小值，求a的取值范围；
（3）若-2＜x1＜0，求b的取值范围．
查看答案和解析>>
科目：高中数学
来源：2010-2011学年江苏省徐州一中高一（上）期中数学试卷（解析版）
题型：解答题
设函数f（x）=ax2+bx+1，a＞0，b∈R 的最小值为-a，f（x）=0两个实根为x1、x2．
（1）求x1-x2的值；
（2）若关于x的不等式f（x）＜0解集为A，函数f（x）+2x在A上不存在最小值，求a的取值范围；
（3）若-2＜x1＜0，求b的取值范围．
查看答案和解析>>
科目：高中数学
来源：2011-2012学年浙江省杭州市余杭高级中学高三（上）第二次段考数学试卷（文科）（解析版）
题型：解答题
设函数f（x）=ax2+bx+1，a＞0，b∈R 的最小值为-a，f（x）=0两个实根为x1、x2．
（1）求x1-x2的值；
（2）若关于x的不等式f（x）＜0解集为A，函数f（x）+2x在A上不存在最小值，求a的取值范围；
（3）若-2＜x1＜0，求b的取值范围．
查看答案和解析>>
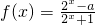（a∈R）的图象关于坐标原点对称
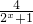-1的零点；
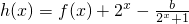在[0，1]内存在零点，求实数b的取值范围
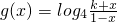，若不等式f-1（x）≤g（x）在
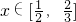上恒成立，求满足条件的最小整数k的值．