
在平面直角坐标系xOy中,点A(5,0),对于某个正实数k,存在函数f(x)=ax2(a>0),使得 (λ为常数),这里点P,Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为 (λ为常数),这里点P,Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为 |
A.(2,+∞) B.(3,+∞) C.[4,+∞) D.[8,+∞) |
科目:高中数学 来源: 题型:
| OP |
| ||
|
|
| ||
|
|
科目:高中数学 来源:2011届重庆市南开中学高三5月月考考试理科数学 题型:单选题
在平面直角坐标系xOy中,点A(5,0),对于某个正实数k,存在函数 ,使得
,使得 (
(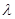 为常数),这里点P、Q的坐标分别为
为常数),这里点P、Q的坐标分别为 ,则k的取值范围为( )
,则k的取值范围为( )
A. | B. | C. | D. |
科目:高中数学 来源:2013-2014学年河南省原名校高三上学期期联考理科数学试卷(解析版) 题型:选择题
在平面直角坐标系xOy中,点A(5,0),对于某个正实数k,存在函数f(x)=a (a>0).使得
(a>0).使得 =λ·(
=λ·( +
+ )(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为(
)
)(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为(
)
A.(2,+∞) B.(3,+∞) C.[4,+∞) D.[8,+∞)
科目:高中数学 来源:2011-2012学年河北省高三上学期期末考试理科数学(解析版) 题型:选择题
在平面直角坐标系xOy中,点A(5,0),对于某个正实数k,存在函数f(x)=ax2
(a>0),使得 (λ为常数),这里点P、Q的坐标分别为
(λ为常数),这里点P、Q的坐标分别为
P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
A、(2,+∞) B、(3,+∞) C、[4,+∞) D、[8,+∞)
科目:高中数学 来源:2010-2011学年重庆市高三5月月考考试理科数学 题型:选择题
在平面直角坐标系xOy中,点A(5,0),对于某个正实数k,存在函数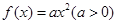 ,使得
,使得 (
( 为常数),这里点P、Q的坐标分别为
为常数),这里点P、Q的坐标分别为 ,则k的取值范围为( )
,则k的取值范围为( )
A. B.
B. C.
C.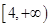 D.
D.
科目:高中数学 来源: 题型:单选题
在平面直角坐标系xOy中,点A(5,0),对于某个正实数k,存在函数f(x)=a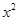 (a>0).使得
(a>0).使得 =λ·(
=λ·( +
+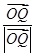 )(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
)(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
| A.(2,+∞) | B.(3,+∞) | C.[4,+∞) | D.[8,+∞) |
科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,点A(5,0),对于某个正实数k,存在函数f(x)=ax2(a>0),使得
 (λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
A、(2,+∞) B、(3,+∞) C、[4,+∞) D、[8,+∞)
科目:高中数学 来源:2012-2013学年浙江省嘉兴市南湖高中高三(上)7月月考数学试卷(文科)(解析版) 题型:选择题
 (λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )科目:高中数学 来源:2011年湖北省华师一附中、荆州中学高考数学模拟试卷(理科)(解析版) 题型:选择题
 (λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )科目:高中数学 来源:2010-2011学年重庆市南开中学高三(下)5月月考数学试卷(理科)(解析版) 题型:选择题
 (λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com