练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若F1，F2为双曲线的左、右焦点，O为坐标原点，点P在双曲线的左支上，点M在双曲线的右准线上，且满足（λ≥0），则该双曲线的离心率为

    A.
    B.
    C.4
    D.2
    D
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：专项题 题型：单选题

    若F1，F2为双曲线的左、右焦点，O为坐标原点，点P在双曲线的左支上，点M在双曲线的右准线上，且满足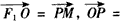（λ≥0），则该双曲线的离心率为
    [     ]
    A.
    B.
    C.4
    D.2

    查看答案和解析>>

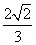
    科目：高中数学 来源：2011年云南省高三数学一轮复习章节练习：双曲线（解析版） 题型：选择题

    若F1、F2为双曲线的左、右焦点，O为坐标原点，点P在双曲线的左支上，点M在双曲线的右准线上，且满足（λ＞0），则该双曲线的离心率为（ ）
    A．
    B．
    C．2
    D．3

    查看答案和解析>>

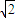
    科目：高中数学 来源： 题型：单选题

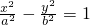    若F1、F2为双曲线数学公式的左、右焦点，O为坐标原点，点P在双曲线的左支上，点M在双曲线的右准线上，且满足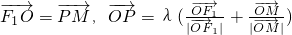数学公式（λ＞0），则该双曲线的离心率为


    1. A.
      数学公式
    2. B.
      数学公式
    3. C.
      2
    4. D.
      3

    查看答案和解析>>

    科目：高中数学 来源：陕西省宝鸡中学2008届高三年级月考(二)数学试卷(理科) 题型：013

    设F1，F2为双曲线的左、右焦点，P为双曲线右支上任一点，若的最小值为8a，则双曲线离心率e的取值范围是

    [　　]

    A．(1，3]

    B．(1，2]

    C．[2，3]

    D．[3，＋∞)

    查看答案和解析>>

    科目：高中数学 来源：陕西省宝鸡中学2008届高三年级月考(二)数学试卷(文科) 题型：013

    设F1，F2为双曲线的左、右焦点，P为双曲线右支上任一点，若的最小值为8a，则双曲线离心率e的取值范围是

    [　　]

    A．(1，3]

    B．(1，2]

    C．[2，3]

    D．[3，＋∞)

    查看答案和解析>>

    科目：高中数学 来源：2012高考数学二轮名师精编精析(15)：圆锥曲线的定义、性质和方程 题型：013

    若F1、F2为双曲线的左、右焦点，O为坐标原点，点P在双曲线的左支上，点M在双曲线的右准线上，且满足：(λ＞0)，则该双曲线的离心率为

    [　　]
    A．

    B．

    C．

    2

    D．

    3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

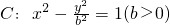    已知点F1，F2为双曲线数学公式的左、右焦点，过F2作垂直于x轴的直线，在x轴上方交双曲线于点M，且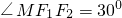数学公式，圆O的方程为x2+y2=b2．
    （1）求双曲线C的方程；
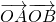    （2）若双曲线C上的点到两条渐近线的距离分别为d1，d2，求d1•d2的值；
    （3）过圆O上任意一点P（x0，y0）作切线l交双曲线C于A，B两个不同点，求数学公式的值．

    查看答案和解析>>

    科目：高中数学 来源：2012年上海市高考数学压轴试卷（文科）（解析版） 题型：解答题

    已知点F1，F2为双曲线的左、右焦点，过F2作垂直于x轴的直线，在x轴上方交双曲线于点M，且，圆O的方程为x2+y2=b2．
    （1）求双曲线C的方程；
    （2）若双曲线C上的点到两条渐近线的距离分别为d1，d2，求d1•d2的值；
    （3）过圆O上任意一点P（x，y）作切线l交双曲线C于A，B两个不同点，求的值．

    查看答案和解析>>

    科目：高中数学 来源：黑龙江省大庆实验中学2010-2011学年高二上学期期末考试数学文科试题 题型：013

    已知F1，F2是双曲线的左、右焦点，P为双曲线左支上一点，若的最小值为8a，则该双曲线的离心率的取值范围是

    [　　]
    A．

    (1，3)

    B．

    (1，2)

    C．

    (1，3]

    D．

    (1，2]

    查看答案和解析>>

    科目：高中数学 来源：2008年广东地区数学科全国各地模拟试题直线与圆锥曲线大题集 题型：044

    如图，若F1、F2为双曲线的左、右焦点，O为坐标原点，P在双曲线左支上，M在右准线上，且四边形OMPF1为菱形．

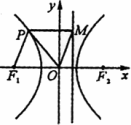
    (Ⅰ)若此双曲线过点，求双曲线的方程；

    (Ⅱ)设(Ⅰ)中双曲线的虚轴端点为B1、B2(B1在y轴的正半轴上)，过B2作直线l与双曲线交于A、B两点，当时，求直线l的方程．

    查看答案和解析>>


    同步练习册答案