
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| x |
| 4 |
| y |
科目:高中数学 来源:不详 题型:单选题
| 1 |
| 2 |
| 1 |
| x |
| 4 |
| y |
| A.8 | B.9 | C.16 | D.18 |
科目:高中数学 来源:2011-2012学年河北省衡水中学高一(下)期末数学试卷(理科)(解析版) 题型:选择题
 ,则
,则 的最小值为( )
的最小值为( )科目:高中数学 来源: 题型:
| 7 |
| cosA |
| cosC |
| ||
2b-
|
| π |
| 6 |
科目:高中数学 来源:不详 题型:解答题
| 7 |
| cosA |
| cosC |
| ||
2b-
|
| π |
| 6 |
科目:高中数学 来源: 题型:
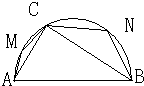 已知 A、B两地相距2R,以AB为直径作一个半圆,在半圆上取一点C,连接AC、BC,在三角形ABC内种草坪(如图),M、N分别为弧AC、弧BC的中点,在三角形AMC、三角形BNC上种花,其余是空地.设花坛的面积为S1,草坪的面积为S2,取∠ABC=θ.
已知 A、B两地相距2R,以AB为直径作一个半圆,在半圆上取一点C,连接AC、BC,在三角形ABC内种草坪(如图),M、N分别为弧AC、弧BC的中点,在三角形AMC、三角形BNC上种花,其余是空地.设花坛的面积为S1,草坪的面积为S2,取∠ABC=θ.| S1 | S2 |
科目:高中数学 来源: 题型:解答题
 已知 A、B两地相距2R,以AB为直径作一个半圆,在半圆上取一点C,连接AC、BC,在三角形ABC内种草坪(如图),M、N分别为弧AC、弧BC的中点,在三角形AMC、三角形BNC上种花,其余是空地.设花坛的面积为S1,草坪的面积为S2,取∠ABC=θ.
已知 A、B两地相距2R,以AB为直径作一个半圆,在半圆上取一点C,连接AC、BC,在三角形ABC内种草坪(如图),M、N分别为弧AC、弧BC的中点,在三角形AMC、三角形BNC上种花,其余是空地.设花坛的面积为S1,草坪的面积为S2,取∠ABC=θ.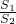 的最小值.
的最小值.科目:高中数学 来源:湖北省模拟题 题型:解答题
 被圆M所截的弦长为
被圆M所截的弦长为 ,且圆心M在直线l的下方.
,且圆心M在直线l的下方.科目:高中数学 来源: 题型:
已知圆M的圆心M在x轴上,半径为1,直线l:y=![]() x-
x-![]() 被圆M所截的弦长为
被圆M所截的弦长为![]() ,且圆心M在直线l的下方.
,且圆心M在直线l的下方.
(1)求圆M的方程;
(2)设A(0,t),B(0,t+6)(-5≤t≤-2),若圆M是△ABC的内切圆,求△ABC的面积S的最大值和最小值.
科目:高中数学 来源:2012-2013学年湖北省襄阳市高二(上)期末数学试卷(文科)(解析版) 题型:解答题
 ,被圆M所截的弦长为
,被圆M所截的弦长为 ,且圆心M在直线l的下方.
,且圆心M在直线l的下方.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com