
科目:初中数学 来源:不详 题型:单选题
| A.6个 | B.7个 | C.8个 | D.9个 |

科目:初中数学 来源:2012-2013学年江苏省扬州市宝应县实验初中八年级(上)纠错练习数学试卷(9月份)(解析版) 题型:选择题

科目:初中数学 来源:模拟题 题型:解答题
科目:初中数学 来源:山东省中考真题 题型:解答题
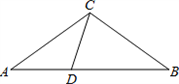
已知:如图,在△ABC中,D为A月边上一点,∠A=36°,AC=BC,AC2=AB·AD。
(1)试说明:△ADC和△BDC都是等腰三角形;
(2)若AB=1,求AC的长;
(3)试构造一个等腰梯形,要求该梯形连同它的两条对角线所形成的8个三角形中有尽可能多的等腰三角形。

科目:初中数学 来源: 题型:
已知:如图,在△ABC中,D为A月边上一点,∠A=36°,AC=BC,AC2=AB?AD.
(1)试说明:△ADC和△BDC都是等腰三角形,
(2)若AB=1,求AC的长,
(3)试构造一个等腰梯形,要求该梯形连同它的两条对角线所形成的8个三角形中有尽可能多的等腰三角形.

科目:初中数学 来源: 题型:
如图2,在△ABC中,AB=AC,∠A=36°,两条角平分线BD、CE相交于点O,则图中全等等腰三角形有 ( )
A.1对 B.2对 C.3对 D.4对

科目:初中数学 来源:2007年德州市初中毕业、升学统一考试数学试卷 题型:044
已知:如图14,在△ABC中,D为AB边上一点,∠A=36°,AC=BC,AC2=AB·AD.
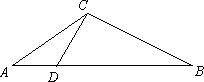
(1)试说明:△ADC和△BDC都是等腰三角形;
(2)若AB=1,求AC的值;
(3)请你构造一个等腰梯形,使得该梯形连同它的两条对角线得到8个等腰三角形.(标明各角的度数)
科目:初中数学 来源: 题型:解答题
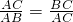 ,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果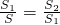 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.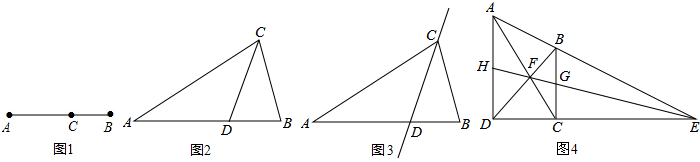
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com