科目：初中数学 来源： 题型：

9、已知M、N、P三点在同一条直线上，如果线段MN=6cm，NP=2cm，那么M，P两点的距离是（　　）

A、8cm

B、4cm

C、8cm或4cm

D、无法确定

查看答案和解析>>

科目：初中数学 来源： 题型：

14、已知A、B、C三点在同一条直线上，如果线段AB=3cm，BC=1cm，那么A、C两点的距离d的长度为（　　）

A、4cm

B、2cm

C、小于或等于4cm，且大于或等于2cm

D、4cm或2cm

查看答案和解析>>

科目：初中数学 来源： 题型：

6、已知A、B、C三点在同一直线上，那么线段AB、BC、AC三者的关系是（　　）

A、AC=AB+BC

B、AC＞AB

C、AC＞AB＞BC

D、不能确定

查看答案和解析>>

科目：初中数学 来源： 题型：

已知平面上有n个点，A、B、C三个点在一条直线上，A、D、F、E四点也在一条直线上，除此之外，只有两点在一条直线上，若以这几个点作直线，那么一共可以画出38条不同的直线，则n=

．

查看答案和解析>>

科目：初中数学 来源： 题型：

已知：如图所示，点C在线段AB上，分别以AC、BC为一边作为等边△ACM和等边△BCN，连接AN、BM．
（1）求证：AN=BM；
（2）设AN、BM相交于点D，求证：∠ADB=120°；
（3）如果A、C、B三点不在同一直线上，那么AN=BM是否仍然成立？如果成立，加以证明；如果不成立，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

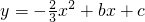已知抛物线 $数学公式$ 与x轴交于不同的两点A（x₁，0）和B（x₂，0），与y轴交于点C，且x₁，x₂是方程x²-2x-3=0的两个根（x₁＜x₂）．
（1）求抛物线的解析式；
（2）过点A作AD∥CB交抛物线于点D，求四边形ACBD的面积；
（3）如果P是线段AC上的一个动点（不与点A、C重合），过点P作平行于x轴的直线l交BC于点Q，那么在x轴上是否存在点R，使得△PQR为等腰直角三角形？若存在，求出点R的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源：2011-2012学年安徽阜阳市七年级数学下学期期末考试数学试卷（带解析） 题型：填空题

已知三点M、N、P不在同一条直线上，且MN=4厘米，NP=3厘米，M、P两点间的距离为x厘米，那么x的取值范围是。

查看答案和解析>>

科目：初中数学 来源：2011-2012学年安徽阜阳七年级下学期期末抽考数学试卷（带解析） 题型：填空题

已知三点M、N、P不在同一条直线上，且MN=4厘米，NP=3厘米，M、P两点间的距离为x厘米，那么x的取值范围是。

查看答案和解析>>

科目：初中数学 来源：2013年江西省抚州市中考数学模拟试卷（二）（解析版） 题型：解答题

已知抛物线

与x轴交于不同的两点A（x₁，0）和B（x₂，0），与y轴交于点C，且x₁，x₂是方程x²-2x-3=0的两个根（x₁＜x₂）．
（1）求抛物线的解析式；
（2）过点A作AD∥CB交抛物线于点D，求四边形ACBD的面积；
（3）如果P是线段AC上的一个动点（不与点A、C重合），过点P作平行于x轴的直线l交BC于点Q，那么在x轴上是否存在点R，使得△PQR为等腰直角三角形？若存在，求出点R的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源：2012年山东省济南市中考数学模拟试卷（十一）（解析版） 题型：解答题

已知抛物线

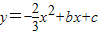与x轴交于不同的两点A（x₁，0）和B（x₂，0），与y轴交于点C，且x₁，x₂是方程x²-2x-3=0的两个根（x₁＜x₂）．
（1）求抛物线的解析式；
（2）过点A作AD∥CB交抛物线于点D，求四边形ACBD的面积；
（3）如果P是线段AC上的一个动点（不与点A、C重合），过点P作平行于x轴的直线l交BC于点Q，那么在x轴上是否存在点R，使得△PQR为等腰直角三角形？若存在，求出点R的坐标；若不存在，请说明理由．

查看答案和解析>>

练习册

高中

初中

小学