
科目:初中数学 来源:不详 题型:单选题

| A.每个点的横坐标加上2 | B.每个点的纵坐标加上2 |
| C.每个点的横坐标减去2 | D.每个点的纵坐标减去2 |
科目:初中数学 来源: 题型:单选题
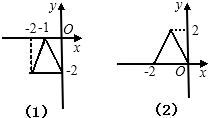
科目:初中数学 来源: 题型:

| (1+2)×2 |
| 2 |
| (1+3)×3 |
| 2 |
| (1+4)×4 |
| 2 |
| (1+4)×4 |
| 2 |
| (1+9)×9 |
| 2 |
| (1+9)×9 |
| 2 |

| (1+n-1)(n-1) |
| 2 |
| (1+n)×n |
| 2 |
| (1+n-1)(n-1) |
| 2 |
| (1+n)×n |
| 2 |
科目:初中数学 来源: 题型:阅读理解
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
科目:初中数学 来源:期中题 题型:解答题
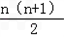 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=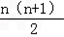 .
.
科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:初中数学 来源: 题型:044
我国著名数学家华罗庚曾说过:撌?毙问鄙僦惫郏?紊偈?蹦讶胛ⅲ皇?谓岷习侔愫茫?衾敕旨彝蚴滦輸.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.
数形结合的基本思想,就是在研究问题的过程中,注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题,或者把数量关系的问题转化为图形性质的问题,使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案.
例如,求1+2+3+4+…+n的值,其中n是正整数.
对于这个求和问题,如果采用纯代数的方法(首尾两头加),问题虽然可以解决,但在求和过程中,需对n的奇偶性进行讨论.
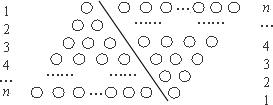
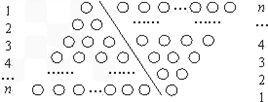
如果采用数形结合的方法,即用图形的性质来说明数量关系的事实,那就非常的直观.现利用图形的性质来求1+2+3+4+…+n 的值,方案如下:如图,斜线左边的三角形图案是由上到下每层依次分别为1,2,3,…,n个小圆圈排列组成的.而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值.为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形.此时,组成平行四边形的小圆圈共有n行,每行有(n+1)个小圆圈,所以组成平行四边形小圆圈的总个数为n(n+1)个,因此,组成一个三角形小圆圈的个数为![]() ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=![]() .
.

(1
)仿照上述数形结合的思想方法,设计相关图形,求1+3+5+7+…+(2n-1)的值,其中 n 是正整数.(要求:画出图形,并利用图形做必要的推理说明)(2
)试设计另外一种图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数.(要求:画出图形,并利用图形做必要的推理说明)科目:初中数学 来源: 题型:阅读理解
我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.
数形结合的基本思想,就是在研究问题的过程中,注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题,或者把数量关系的问题转化为图形性质的问题,使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案.
例如,求1+2+3+4+…+n的值,其中n是正整数.
对于这个求和问题,如果采用纯代数的方法(首尾两头加),问题虽然可以解决,但在求和过程中,需对n的奇偶性进行讨论.
如果采用数形结合的方法,即用图形的性质来说明数量关系的事实,那就非常的直观.现利用图形的性质来求1+2+3+4+…+n 的值,方案如下:如图,斜线左边的三角形图案是由上到下每层依次分别为1,2,3,…,n个小圆圈排列组成的.而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值.为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形.此时,组成平行四边形的小圆圈共有n行,每行有(n+1)个小圆圈,所以组成平行四边形小圆圈的总个数为n(n+1)个,因此,组成一个三角形小圆圈的个数为![]() ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=![]() .
.

(1)仿照上述数形结合的思想方法,设计相关图形,求1+3+5+7+…+(2n-1)的值,其中 n 是正整数.(要求:画出图形,并利用图形做必要的推理说明)
(2)试设计另外一种图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数.(要求:画出图形,并利用图形做必要的推理说明)
科目:初中数学 来源: 题型:044
我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.
数形结合的基本思想,就是在研究问题的过程中,注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题,或者把数量关系的问题转化为图形性质的问题,使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案.
例如,求1+2+3+4+…+n的值,其中n是正整数.
对于这个求和问题,如果采用纯代数的方法(首尾两头加),问题虽然可以解决,但在求和过程中,需对n的奇偶性进行讨论.
如果采用数形结合的方法,即用图形的性质来说明数量关系的事实,那就非常的直观.现利用图形的性质来求1+2+3+4+…+n 的值,方案如下:如图,斜线左边的三角形图案
是由上到下每层依次分别为1,2,3,…,n个小圆圈排列组成的.而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值.为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形.此时,组成平行四边形的小圆圈共有n行,每行有(n+1)个小圆圈,所以组成平行四边形小圆圈的总个数为n(n+1)个,因此,组成一个三角形小圆圈的个数为![]() ,即
,即![]() .
.

(1)
仿照上述数形结合的思想方法,设计相关图形,求1+3+5+7+…+(2n-1)的值,其中 n 是正整数.(要求:画出图形,并利用图形做必要的推理说明)(2)
试设计另外一种图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数.(要求:画出图形,并利用图形做必要的推理说明)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com