
科目:初中数学 来源: 题型:解答题
 阅读下列材料,回答问题.
阅读下列材料,回答问题.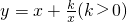 的函数称为“根号函数”,这类函数的图象关于原点中心对称.
的函数称为“根号函数”,这类函数的图象关于原点中心对称.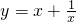 在第一象限内的大致图象如图所示,试在网格内画出该函数在第三象限内的大致图象;
在第一象限内的大致图象如图所示,试在网格内画出该函数在第三象限内的大致图象;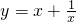 的最小值为2.
的最小值为2.科目:初中数学 来源: 题型:解答题
定义1:在△ABC中,若顶点A,B,C按逆时针方向排列,则规定它的面积为“有向面积”;若顶点A,B,C按顺时针方向排列,则规定它的面积的相反数为△ABC的“有向面积”.“有向面积”用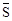 表示,例如图1中,
表示,例如图1中,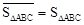 ,图2中,
,图2中,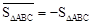 .
.
定义2:在平面内任取一个△ABC和点P(点P不在△ABC的三边所在直线上),称有序数组(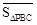 ,
,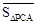 ,
,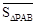 )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作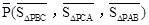 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2,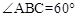 ,则
,则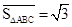 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标”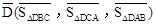 为
为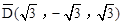 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: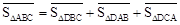 .
.
应用新知:
(1)如图4,正方形ABCD的边长为1,则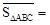 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现:
(2)在平面直角坐标系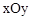 中,点
中,点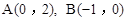 ,
,
①若点P是第二象限内任意一点(不在直线AB上),设点P关于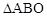 的“面积坐标”为
的“面积坐标”为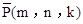 ,
,
试探究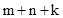 与
与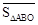 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点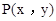 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于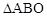 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);
解决问题:
(3)在(2)的条件下,点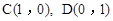 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.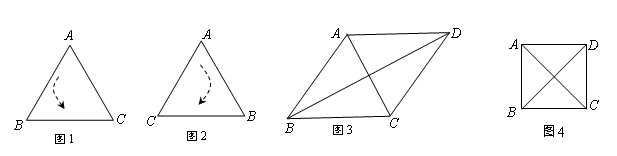
科目:初中数学 来源:不详 题型:解答题
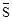 表示,例如图1中,
表示,例如图1中,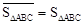 ,图2中,
,图2中,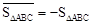 .
.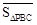 ,
,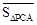 ,
,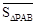 )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作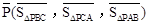 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2,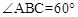 ,则
,则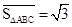 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标”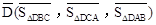 为
为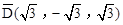 .在图3中,我们知道
.在图3中,我们知道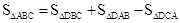 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: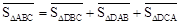 .
.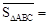 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现: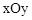 中,点
中,点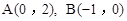 ,
,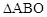 的“面积坐标”为
的“面积坐标”为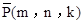 ,
,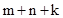 与
与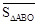 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;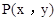 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于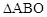 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);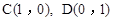 ,点Q在抛物线
,点Q在抛物线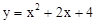 上,求当
上,求当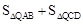 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.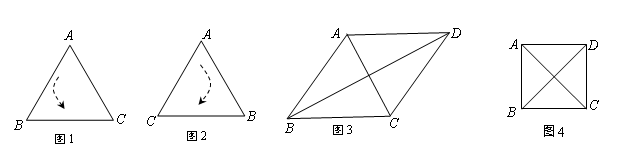
科目:初中数学 来源: 题型:
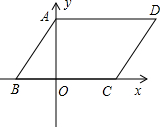 x2-7x+12=0的两个根,且OA>OB.
x2-7x+12=0的两个根,且OA>OB.科目:初中数学 来源: 题型:
如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程![]() 的两个根,且
的两个根,且![]() 。
。

(1)则点C的坐标是_____________,点D的坐标是__________;
(2)若将此平行四边形ABCD沿x轴正方向向右平移3个单位,沿y轴正方向向上平移2个单位,则点C的坐标是____________,点D的坐标是_________;
(3)若将平行四边形ABCD平移到第一象限后,点B的坐标是(a,b),则点C的坐标是________,点D的坐标是_______;
(4)若点M在平面直角坐标系内,则在上图的直线AB上,并且在第一、第二象限内是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由。
科目:初中数学 来源: 题型:
 如图,直线y=0.75x+6与x轴、y轴分别交于点E、F,点E的坐标为(-8,0),点P(x,y)是第二象限内的直线上的一个动点,则△OPE的面积S与x的函数关系式为
如图,直线y=0.75x+6与x轴、y轴分别交于点E、F,点E的坐标为(-8,0),点P(x,y)是第二象限内的直线上的一个动点,则△OPE的面积S与x的函数关系式为科目:初中数学 来源: 题型:填空题
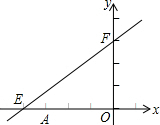 如图,直线y=0.75x+6与x轴、y轴分别交于点E、F,点E的坐标为(-8,0),点P(x,y)是第二象限内的直线上的一个动点,则△OPE的面积S与x的函数关系式为________.
如图,直线y=0.75x+6与x轴、y轴分别交于点E、F,点E的坐标为(-8,0),点P(x,y)是第二象限内的直线上的一个动点,则△OPE的面积S与x的函数关系式为________.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com