
科目:初中数学 来源:不详 题型:单选题
| 2 |
| x |
| 2 |
| 2 |
| A.0个 | B.1个 | C.2个 | D.3个 |
科目:初中数学 来源: 题型:
| 2 |
| x |
| 2 |
| 2 |
科目:初中数学 来源:2004年江苏省南京市师范大学附属扬子中学中考数学试卷(解析版) 题型:选择题
科目:初中数学 来源: 题型:解答题
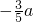 ,0)
,0)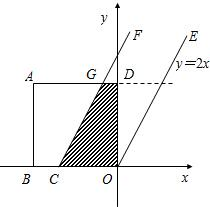 且与OE平行,现正方形以每秒
且与OE平行,现正方形以每秒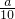 的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S.
的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S.科目:初中数学 来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版) 题型:解答题
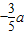 ,0)且与OE平行,现正方形以每秒
,0)且与OE平行,现正方形以每秒 的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S.
的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S.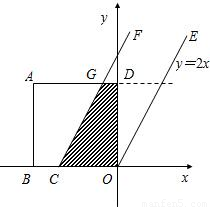
科目:初中数学 来源:第34章《二次函数》常考题集(25):34.4 二次函数的应用(解析版) 题型:解答题
 ,0)且与OE平行,现正方形以每秒
,0)且与OE平行,现正方形以每秒 的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S.
的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S.
科目:初中数学 来源:第2章《二次函数》常考题集(25):2.3 二次函数的应用(解析版) 题型:解答题
 ,0)且与OE平行,现正方形以每秒
,0)且与OE平行,现正方形以每秒 的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S.
的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S.
科目:初中数学 来源:第6章《二次函数》常考题集(25):6.4 二次函数的应用(解析版) 题型:解答题
 ,0)且与OE平行,现正方形以每秒
,0)且与OE平行,现正方形以每秒 的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S.
的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S.
科目:初中数学 来源:第26章《二次函数》常考题集(24):26.3 实际问题与二次函数(解析版) 题型:解答题
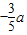 ,0)且与OE平行,现正方形以每秒
,0)且与OE平行,现正方形以每秒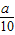 的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S.
的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S.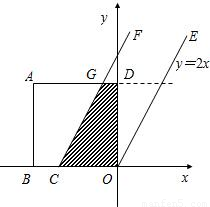
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com