
科目:初中数学 来源: 题型:单选题
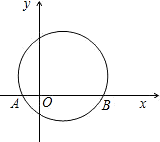 如图,圆不能表示y是x的函数图象,是因为
如图,圆不能表示y是x的函数图象,是因为科目:初中数学 来源:2012-2013学年北京市十五中九年级(上)期中数学试卷(解析版) 题型:选择题
 上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH=
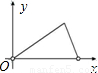
上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH= DE.设EC的长为x,△CEH的面积为y,选项中表示y与x的函数关系式的图象可能是( )
DE.设EC的长为x,△CEH的面积为y,选项中表示y与x的函数关系式的图象可能是( )



科目:初中数学 来源:2011年山东省泰安市肥城市马埠中学中考数学模拟试卷(五)(解析版) 题型:选择题
 上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH=
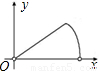
上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH= DE.设EC的长为x,△CEH的面积为y,选项中表示y与x的函数关系式的图象可能是( )
DE.设EC的长为x,△CEH的面积为y,选项中表示y与x的函数关系式的图象可能是( )



科目:初中数学 来源:2011年北京市朝阳区中考数学二模试卷(解析版) 题型:选择题
 上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH=
上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH= DE.设EC的长为x,△CEH的面积为y,选项中表示y与x的函数关系式的图象可能是( )
DE.设EC的长为x,△CEH的面积为y,选项中表示y与x的函数关系式的图象可能是( )




科目:初中数学 来源: 题型:单选题
 如图,扇形OAB的半径OA=6,圆心角∠AOB=90°,C是
如图,扇形OAB的半径OA=6,圆心角∠AOB=90°,C是 上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH=
上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH= DE.设EC的长为x,△CEH的面积为y,选项中表示y与x的函数关系式的图象可能是
DE.设EC的长为x,△CEH的面积为y,选项中表示y与x的函数关系式的图象可能是

科目:初中数学 来源: 题型:
如图,以![]() 为圆心作⊙
为圆心作⊙![]() ,⊙
,⊙![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() .
. ![]() 为⊙
为⊙![]() 上不同于
上不同于![]() 、
、![]() 的任意一点.连接
的任意一点.连接![]() 、
、![]() ,过点
,过点![]() 分别作
分别作![]() 于
于![]() ,
,![]() 于
于![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() .当点
.当点![]() 在⊙
在⊙![]() 上顺时针从点
上顺时针从点![]() 运动到点
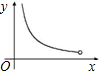
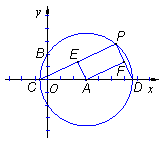
运动到点![]() 的过程中,下列图象中,能表示
的过程中,下列图象中,能表示![]() 与
与![]() 的函数关系的图象是( )
的函数关系的图象是( )
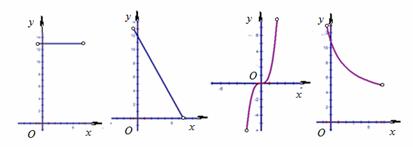
A. B. C. D.
科目:初中数学 来源: 题型:044
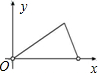
撊?确纸菙是数学史上一个著名问题,但仅用尺规不可能撊?确纸菙 .下面是数学家帕普斯借助函数给出的一种撊?确秩窠菗的方法(如图),将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数![]() 的图象交于点P,以P为圆心,以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到得到∠MOB,则
的图象交于点P,以P为圆心,以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到得到∠MOB,则![]() .要明白帕普斯的方法,请你研究以下问题:
.要明白帕普斯的方法,请你研究以下问题:
(1)设![]() 、
、![]() ,求直线OM相对应的函数解析式(用含a,b的代数式表示).
,求直线OM相对应的函数解析式(用含a,b的代数式表示).
(2)分别过P和R作y轴和x轴的平行线,两直线相交于点Q,请说明Q点在直线OM上,据此证明![]() .
.
(3)应用上述方法得到结论,你如何三等分一个钝角(用文字简要说明).

科目:初中数学 来源:第1章《反比例函数》中考题集(26):1.3 实际生活中的反比例函数(解析版) 题型:解答题
 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: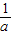 )、R(b,
)、R(b, ),求直线OM对应的函数表达式(用含a,b的代数式表示);
),求直线OM对应的函数表达式(用含a,b的代数式表示); ∠AOB;
∠AOB;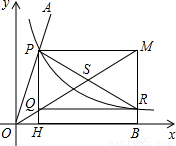
科目:初中数学 来源:2011-2012学年北师大版九年级(上)期末数学试卷(八)(解析版) 题型:解答题
 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: )、R(b,
)、R(b, ),求直线OM对应的函数表达式(用含a,b的代数式表示);
),求直线OM对应的函数表达式(用含a,b的代数式表示); ∠AOB;
∠AOB;
科目:初中数学 来源:2006-2007学年湖北省潜江市九年级(上)期末数学试卷(解析版) 题型:解答题
 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: )、R(b,
)、R(b, ),求直线OM对应的函数表达式(用含a,b的代数式表示);
),求直线OM对应的函数表达式(用含a,b的代数式表示); ∠AOB;
∠AOB;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com