
科目:初中数学 来源:四川省宜宾市2012年中考数学试题 题型:044
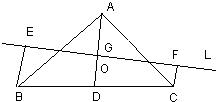
如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE、始终经过点A,EF与AC交于M点.

(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当线段AM最短时,求重叠部分的面积.
科目:初中数学 来源: 题型:

科目:初中数学 来源: 题型:解答题
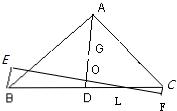
 如图,在平面直角坐标系中,△ABCS三个顶点的坐标分别为A(-6,0),B(6,0),C(0,m)(其中m>0),延长AC到点D,使CD=
如图,在平面直角坐标系中,△ABCS三个顶点的坐标分别为A(-6,0),B(6,0),C(0,m)(其中m>0),延长AC到点D,使CD= AC,过点D作DE∥AB交BC的延长线于点E.
AC,过点D作DE∥AB交BC的延长线于点E.科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,有一条直线l:![]() 与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移.
与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移.
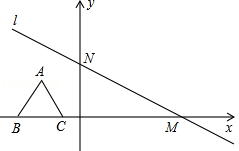
(1)在平移过程中,得到△A1B1C1,此时顶点A1恰落在直线l上,写出A1点的坐标 ;
(2)继续向右平移,得到△A2B2C2,此时它的外心P恰好落在直线l上,求P点的坐标;
(3)在直线l上是否存在这样的点,与(2)中的A2、B2、C2任意两点能同时构成三个等腰三角形?如果存在,求出点的坐标;如果不存在,说明理由.
科目:初中数学 来源:2013年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系中,有一条直线l: 与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移.
与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移.

(1)在平移过程中,得到△A1B1C1,此时顶点A1恰落在直线l上,写出A1点的坐标 ;
(2)继续向右平移,得到△A2B2C2,此时它的外心P恰好落在直线l上,求P点的坐标;
(3)在直线l上是否存在这样的点,与(2)中的A2、B2、C2任意两点能同时构成三个等腰三角形?如果存在,求出点的坐标;如果不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com