
科目:初中数学 来源: 题型:
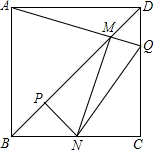 如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=
如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=| 1 |
| 2 |
| AB+BN |
| BM |
| A、①②③ | B、①②④ |
| C、②③④ | D、①②③④ |
科目:初中数学 来源:不详 题型:单选题
| 1 |
| 2 |
| AB+BN |
| BM |
| A.①②③ | B.①②④ | C.②③④ | D.①②③④ |

科目:初中数学 来源:2012年浙江省杭州市中考数学模拟试卷(4)(解析版) 题型:选择题
 BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④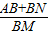 为定值.其中一定成立的是( )
为定值.其中一定成立的是( )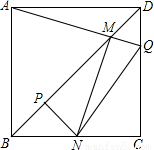
科目:初中数学 来源: 题型:单选题
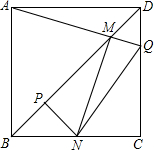 如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=
如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP= BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④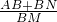 为定值.其中一定成立的是
为定值.其中一定成立的是科目:初中数学 来源:河北省邯郸市2010届九年级一模考试数学试题 题型:059
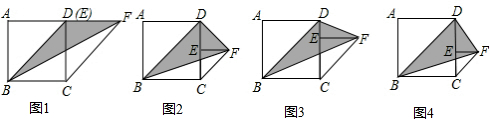
已知:正方形ABCD的边长为a,P是边CD上一个动点不与C、D重合,CP=b,以CP为一边在正方形ABCD外作正方形PCEF,连结BF、DF.

观察计算:
(1)如图,当a=4,b=1时,四边形ABFD的面积为________;

(2)如图,当a=4,b=2时,四边形ABFD的面积为________;

(3)如图,当a=4,b=3时,四边形ABFD的面积为________;

探索发现:
(4)根据上述计算的结果,你认为四边形ABFD的面积与正方形ABCD的面积之间有怎样的关系?证明你的结论.
综合应用:
(5)农民赵大伯有一块正方形的土地(如图),由于修路被占去一块三角形的地方△BCE,但决定在DE的右侧补给赵大伯一块土地,补偿后的土地为四边形ABMD,且四边形ABMD的面积与原来正方形土地的面积相等,M、E、B三点要在一条直线上,请你画图说明,如何确定M点的位置.

科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
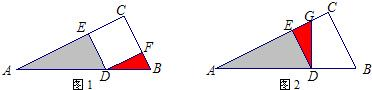
科目:初中数学 来源: 题型:
在平面内,旋转变换是指某一图形绕一个定点按顺时针或逆时针旋转一定的角度得到新位置图形的一种变换.
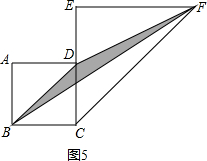
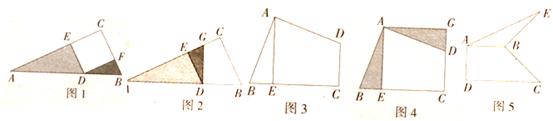
活动一:如图l,在Rt△ABC中,D为斜边AB上的一点,AD =2,BD =1,且四边形DECF是正方形,在求阴影部分面积时,小明运用图形旋转的方法,将△DBF绕点D逆时针旋转90°,得到△DGE(如图2所示),小明一眼就看出答案,请你写出阴影部分的面积:________.
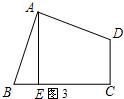
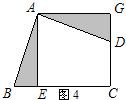
活动二:如图3,在四边形ABCD中,AB=AD,∠BAD=∠C=90°,BC =5,CD =3,过点A作AE⊥BC,垂足为点E,小明仍运用图形旋转的方法,将△ABE绕点A逆时针旋转90°,得到△ADC(如图4所示),则:
(1)四边形AECG是怎样的特殊四边形?答:___________;
(2)AE的长是______________.
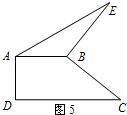
活动三:如图5,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC绕点B逆时针旋转90°得到线段BE,连结AE.若AB =2,DC =4,求△ABE的面积.
科目:初中数学 来源: 题型:
科目:初中数学 来源:2011年安徽省泗县初二上学期期末数学卷 题型:解答题
在平面内,旋转变换是指某一图形绕一个定点按顺时针或逆时针旋转一定的角度得到新位置图形的一种变换.
活动一:如图l,在Rt△ABC中,D为斜边AB上的一点,AD =2,BD =1,且四边形DECF是正方形,在求阴影部分面积时,小明运用图形旋转的方法,将△DBF绕点D逆时针旋转90°,得到△DGE(如图2所示),小明一眼就看出答案,请你写出阴影部分的面积:________.
活动二:如图3,在四边形ABCD中,AB=AD,∠BAD=∠C=90°,BC =5,CD =3,过点A作AE⊥BC,垂足为点E,小明仍运用图形旋转的方法,将△ABE绕点A逆时针旋转90°,得到△ADC(如图4所示),则:
(1)四边形AECG是怎样的特殊四边形?答:___________;
(2)AE的长是______________.
活动三:如图5,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC绕点B逆时针 旋转90°得到线段BE,连结AE.若AB =2,DC =4,求△ABE的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com