在△ABC中，DE是中位线，∠B的平分线交DE于F，则△ABF一定是

1. A.
   锐角三角形
2. B.
   直角三角形
3. C.
   钝角三角形
4. D.
   直角三角形或钝角三角形

在△ABC中，点O是AC边上一动点，点P在BC延长线上，过点O的直线DE∥BC交∠ACB与∠ACP的平分线于点D、E．
（1）点O在什么位置时，四边形ADCE是矩形？说明理由．
（2）在（1）的条件下，当AC与BC满足什么条件时，四边形ADCE是正方形？为什么？

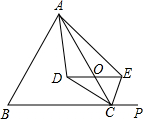
如图，△ABC中，点O是AC边上一动点，点P在BC延长线上，过点O的直线DE∥BC交∠ACB与∠ACP的平分线于D、E，

(1)点O在什么位置时，四边形ADCE是矩形？试说明理由．

(2)在(1)的条件下，当AC与BC满足什么条件时，四边形ADCE是正方形？并说明理由．

已知在梯形ABCD中，AD∥BC,AB=AD,∠BAD的平分线交BC边于点E，连接DE.

（1）求证：四边形ABED是菱形；

（2）若∠ABC=60°,EC=2BE,判断DE和DC的位置关系，并证明之.

Rt△ABC与Rt△FED是两块全等的含30^o、60^o角的三角板，按如图（一）所示拼在一起，CB与DE重合．

1.求证：四边形ABFC为平行四边形

2.取BC中点O，将△ABC绕点O顺时针方向旋转到如图（二）中△位置，直线与AB、CF分别相交于P、Q两点，猜想OQ、OP长度的大小关系，并证明你的猜想．

3.在(2)的条件下,指出当旋转角为多少度时,四边形PCQB为菱形(不要求证明).