若1、2、3、x的平均数是6；1、2、3、x、y的平均数是7，则y的值为

A.
7
B.
9
C.
11
D.
13

查看答案和解析>>

科目：初中数学 来源：同步题 题型：单选题

[ ]

A．7
B．9
C．11
D．13

查看答案和解析>>

科目：初中数学 来源：中学教材全解　七年级数学下　(北京师大版) 北京师大版 题型：044

甲、乙两人接着做如下的游戏：如图是一个均匀的小立方体，立方体的每个面上分别标有数字1，2，3，4，5，6．任意掷出小立方体后，若朝上的数字是6，则甲获胜；若朝上的数字不是6，则乙获胜．

你认为这个游戏对甲、乙双方公平吗？

查看答案和解析>>

科目：初中数学 来源：新教材新学案数学九年级上册 题型：044

甲、乙两人玩掷骰子游戏，为了使游戏不含人为因素，除了骰子要均匀外，还要注意骰子从一定的高度任意抛出．游戏规则是：若甲掷出后骰子停止转动质数点朝上就得1分，否则不得分；乙掷出后骰子停止转动合数点朝上就得1分，否则不得分．两人各掷20次，记录每次得分的结果，得分高的人为胜者．(1)问这个游戏对甲、乙双方公平吗？

请说说你的理由；如果不公平请你利用这个游戏设计一个公平的游戏，说说你的方法．

查看答案和解析>>

科目：初中数学 来源：101网校同步练习　初一数学　华东师大(新课标2001-3年初审) 华东师大(新课标2001-3年初审) 题型：022

已知x₁、x₂、x₃的平均数是a，则3x₁＋2，3x₂＋2，3x₃＋2的平均数是________；若3x₁＋2，3x₂＋2，3x₃＋2的平均数是a，则x₁，x₂，x₃的平均数是________．

查看答案和解析>>

科目：初中数学 来源： 题型：

锐角为45°的直角三角形的两直角边长也相等，这样的三角形称为等腰直角三角形．我们常用的三角板中有一块就是这样的三角形，也可称它为等腰直角三角板．把两块全等的等腰直角三角板按如图1放置，其中边BC、FP均在直线l上，边EF与边AC重合．
（1）将△EFP沿直线l向左平移到图2的位置时，EP交AC于点Q，连接AP，BQ．猜想并写出BQ与AP所满足的数量关系和位置关系，请证明你的猜想；
（2）将△EFP沿直线l向左平移到图3的位置时，EP的延长线交AC的延长线于点Q，连接AP，BQ．你认为（1）中所猜想的BQ与AP的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由．

查看答案和解析>>

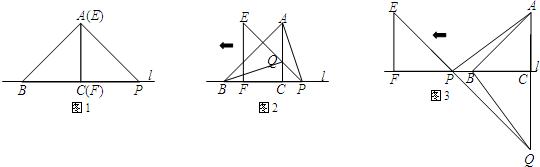
科目：初中数学 来源：江苏期末题 题型：解答题

如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上。
（1）若点P在图中所给网格中的格点上，△APB是等腰三角形，满足条件的点P共有____个；
（2）将线段沿x轴向右平移2格得线段CD，请你求出线段CD所在的直线函数解析式。

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

锐角为45°的直角三角形的两直角边长也相等，这样的三角形称为等腰直角三角形．我们常用的三角板中有一块就是这样的三角形，也可称它为等腰直角三角板．把两块全等的等腰直角三角板按如图1放置，其中边BC、FP均在直线l上，边EF与边AC重合．
（1）将△EFP沿直线l向左平移到图2的位置时，EP交AC于点Q，连接AP，BQ．猜想并写出BQ与AP所满足的数量关系和位置关系，请证明你的猜想；
（2）将△EFP沿直线l向左平移到图3的位置时，EP的延长线交AC的延长线于点Q，连接AP，BQ．你认为（1）中所猜想的BQ与AP的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由．

查看答案和解析>>

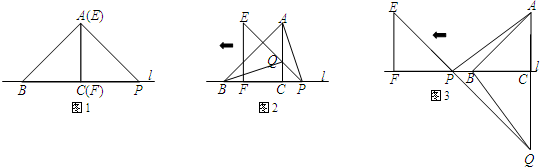
科目：初中数学 来源：江苏省期末题 题型：解答题

锐角为45°的直角三角形的两直角边长也相等，这样的三角形称为等腰直角三角形．我们常用的三角板中有一块就是这样的三角形，也可称它为等腰直角三角板．把两块全等的等腰直角三角板按如图1放置，其中边BC、FP均在直线l上，边EF与边AC重合．
（1）将△EFP沿直线l向左平移到图2的位置时，EP交AC于点Q，连接AP，BQ．猜想并写出BQ与AP所满足的数量关系和位置关系，请证明你的猜想；
（2）将△EFP沿直线l向左平移到图3的位置时，EP的延长线交AC的延长线于点Q，连接AP，BQ．你认为（1）中所猜想的BQ与AP的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由．

查看答案和解析>>

练习册

高中

初中

小学

若1、2、3、x的平均数是6；1、2、3、x、y的平均数是7，则y的值为