
科目:初中数学 来源:第24章《图形的相似》中考题集(25):24.4 中位线(解析版) 题型:选择题
科目:初中数学 来源:单元双测 同步达标活页试卷 八年级数学下 国标人教版 题型:013
依次连接对角线互相垂直的四边形各边中点所成的四边形是
A.等腰梯形
B.矩形
C.菱形
D.正方形
科目:初中数学 来源: 题型:
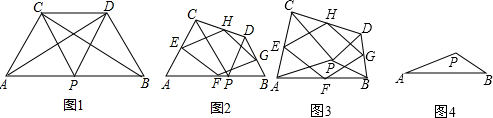
科目:初中数学 来源: 题型:解答题

科目:初中数学 来源:2011年河南省中招押题数学试卷(一)(解析版) 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com