
科目:初中数学 来源: 题型:
| 1 | 2 |
 1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.
1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.科目:初中数学 来源: 题型:解答题
 x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒
x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒 1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.
1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.科目:初中数学 来源:广西自治区中考真题 题型:解答题

科目:初中数学 来源: 题型:
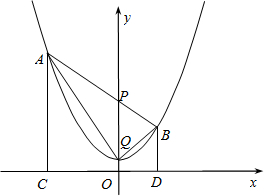
如图,已知点A(−3,5)在抛物线y=![]() x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
1.求抛物线的解析式;
2.当A、Q、B三点构成以AQ为直角边的直角三角形时,求点P离开点Q多少时间?
3.试探索当AP、AC、BP、BD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)时,点P离开点Q的时刻.

科目:初中数学 来源: 题型:
 x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
科目:初中数学 来源:2012年江苏省太仓市初中毕业暨升学考试模拟数学试卷(带解析) 题型:解答题
如图,已知点A(?3,5)在抛物线y= x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
【小题1】求抛物线的解析式;
【小题2】当A、Q、B三点构成以AQ为直角边的直角三角形时,求点P离开点Q多少时间?
【小题3】试探索当AP、AC、BP、BD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)时,点P离开点Q的时刻.
科目:初中数学 来源:2012届江苏省吴江市九年级5月教学调研测试数学试卷(带解析) 题型:解答题
如图,已知点A(?3,5)在抛物线y= x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以
x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以
每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂
足为C、D,连结AQ、BQ.
(1)求抛物线的解析式;
(2)当A、Q、B三点构成以AQ为直角边的直角三角形时,求点P离开点Q多少时间?
(3)试探索当AP、AC、BP、BD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)时,点P离开点Q的时刻.
科目:初中数学 来源:2012年江苏省苏州市太仓市中考数学模拟试卷(解析版) 题型:解答题
 x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.
x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com