
科目:初中数学 来源: 题型:
| 4 |
| 9 |
| 4 |
| 9 |
科目:初中数学 来源: 题型:
按要求画图(要用铅笔和直尺画图并保留画图痕迹)
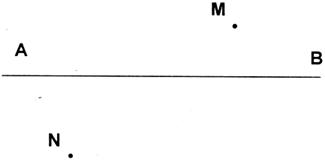
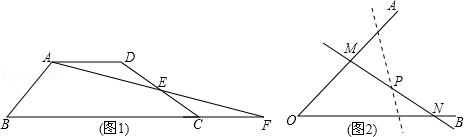
(1)如图,平面内的线段AB,BC,CD,DA首尾相接,按照下列要求画图:
①连接AC,BD相交于点O;
②分别延长线段AD,BC相交于点P;
③分别延长线段BA,CD相交于点Q.

(2)如图,AB表示一条公路,公路两旁分别有一个工厂M和N.要在公路旁建一个货场,使它到M,N两点距离之和最小,货场应建在哪里?在图上画出表示货场位置的点.保留画图痕迹,并回答下列问题:你画图得到点P的依据是______________________________.
科目:初中数学 来源:山东省期中题 题型:操作题
按要求画图(要用铅笔和直尺画图并保留画图痕迹)
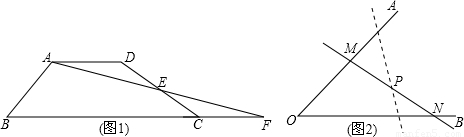
(1)如图,平面内的线段AB,BC,CD,DA首尾相接,按照下列要求画图:
①连接AC,BD相交于点O;
②分别延长线段AD,BC相交于点P;
③分别延长线段BA,CD相交于点Q
(2)如图,AB表示一条公路,公路两旁分别有一个工厂M和N,要在公路旁建一个货场,使它到M,N两点距离之和最小,货场应建在哪里?在图上画出表示货场位置的点.保留画图痕迹,并回答下列问题:你画图得到点P的依据是 _________ 。

科目:初中数学 来源: 题型:
 按要求画图(要用铅笔和直尺画图并保留画图痕迹)
按要求画图(要用铅笔和直尺画图并保留画图痕迹)科目:初中数学 来源:不详 题型:解答题

科目:初中数学 来源:2013年江苏省连云港市中考数学试卷(解析版) 题型:解答题
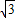 ≈1.73)
≈1.73) ,
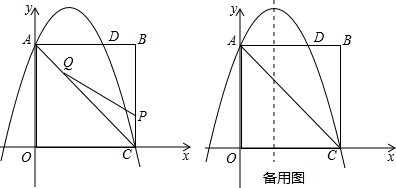
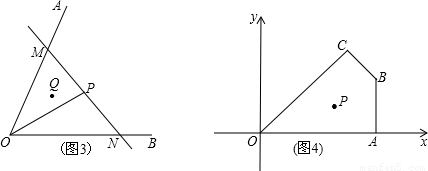
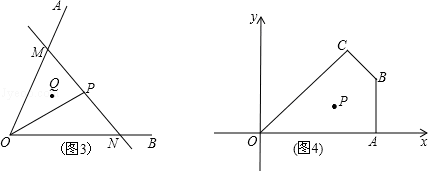
, )、(4、2),过点p的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.
)、(4、2),过点p的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.科目:初中数学 来源:不详 题型:解答题
 ≈1.73)
≈1.73) ,
, )、(4、2),过点p的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.
)、(4、2),过点p的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com