
科目:初中数学 来源:不详 题型:单选题
| A.增加 180° | B.减少 180° |
| C.不变 | D.以上三种情况都有可能 |
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:

科目:初中数学 来源:2010年上海市奉贤区曙光中学中考数学模拟试卷(解析版) 题型:解答题

科目:初中数学 来源: 题型:解答题
科目:初中数学 来源:期末题 题型:操作题
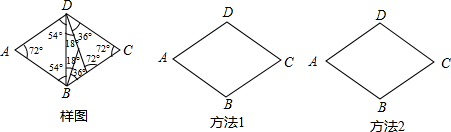
已知,如图,在四边形ABCD中,AB=BC=CD=DA,∠A=∠C=72°,请设计两种不同的分法,将四边形ABCD分割成四个三角形,使得分割成的每个三角形都是等腰三角形,画法要求如下:
(1)两种分法只要有一条分割线段位置不同,就认为是两种不同的分法;
(2)画图工具不限,但要求画出分割线段;
(3)标出能够说明不同分法所得三角形的内角度数,例如样图;
(4)不要求写出画法,不要求证明.


科目:初中数学 来源:不详 题型:解答题

科目:初中数学 来源: 题型:
已知,如图,在四边形ABCD中,AB=BC=CD=DA,∠A=∠C=72°. 请设计两种不同的分法,将四边形ABCD分割成四个三角形,使得分割成的每个三角形都是等腰三角形.画法要求如下:
(1)两种分法只要有一条分割线段位置不同,就认为是两种不同的分法;
(2)画图工具不限,但要求画出分割线段;
(3)标出能够说明不同分法所得三角形的内角度数,例如样图;
(4)不要求写出画法,不要求证明.

科目:初中数学 来源: 题型:
| AC |
| AB |
| BC |
| AC |
| S1 |
| S |
| S2 |
| S1 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com