
科目:初中数学 来源:《24.3 正多边形与圆》2010年同步练习2(解析版) 题型:选择题
科目:初中数学 来源:上海模拟 题型:单选题
| A.每个内角都是120°的六边形一定是正六边形 |
| B.正n边形有n条对称轴 |
| C.正n边形的每一个外角度数等于它的中心角度数的二倍 |
| D.正多边形一定既是轴对称图形,又是中心对称图形 |
科目:初中数学 来源:2004年上海市民办中学“八校联考”中考数学试卷(解析版) 题型:选择题
科目:初中数学 来源: 题型:
| d | R |
科目:初中数学 来源: 题型:解答题
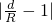 .分别计算n=3,n=6时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
.分别计算n=3,n=6时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?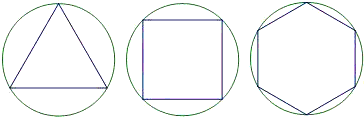
科目:初中数学 来源: 题型:
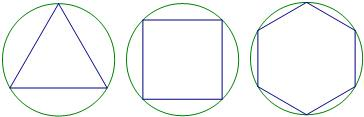
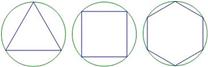
如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”。
(1)角的“接近度”定义:设正n边形的每个内角的度数为m°,将正n边形的“接近度”定义为|180-m|.于是,|180-m|越小,该正n边形就越接近于圆,
①若n=3,则该正n边形的“接近度”等于 。
②若n=20,则该正n边形的“接近度”等于 。
③当“接近度”等于 。 时,正n边形就成了圆.
(2)边的“接近度”定义:设一个正n边形的外接圆的半径为R,正n边形的中心到各边的距离为d,将正n边形的“接近度”定义为![]() .分别计算n=3,n=6时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
.分别计算n=3,n=6时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
科目:初中数学 来源:2011年浙江省杭州市中考数学模拟试卷(17)(解析版) 题型:解答题
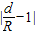 .分别计算n=3,n=6时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
.分别计算n=3,n=6时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?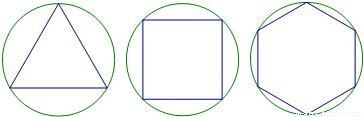
科目:初中数学 来源: 题型:
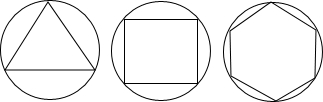 法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.
法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com