
科目:初中数学 来源:不详 题型:单选题
| A.对顶角相等 |
| B.两条直线被第三条直线所截,内错角相等 |
| C.∵∠1=∠2,∠2=∠3,∴∠1=∠3 |
| D.两直线平行,同位角相等 |
科目:初中数学 来源:不详 题型:单选题
| A.全等三角形是指边、角分别对应相等的两个(或两个以上)的三角形 |
| B.两边夹一角对应相等的两个三角形全等 |
| C.有两边和一角对应相等的两个三角形全等 |
| D.符号“SAS”表示判定两个三角形全等的边有两边和夹角对应相等的两个三角形全等 |
科目:初中数学 来源: 题型:阅读理解
【考点】菱形的性质;全等三角形的判定与性质;等边三角形的判定与性质.
【分析】根据菱形的四条边都相等,先判定△ABD是等边三角形,再根据菱形的性质可得∠BDF=∠C=60°,再求出DF=CE,然后利用“边角边”即可证明△BDF≌△DCE,从而判定①正确;根据全等三角形对应角相等可得∠DBF=∠EDC,然后利用三角形的一个外角等于与它不相邻的两个内角的和可以求出∠DMF=∠BDC=60°,再根据平角等于180°即可求出∠BMD=120°,从而判定②正确;根据三角形的一个外角等于与它不相邻的两个内角的和以及平行线的性质求出∠ABM=∠ADH,再利用“边角边”证明△ABM和△ADH全等,根据全等三角形对应边相等可得AH=AM,对应角相等可得∠BAM=∠DAH,然后求出∠MAH=∠BAD=60°,从而判定出△AMH是等边三角形,判定出③正确;根据全等三角形的面积相等可得△AMH的面积等于四边形ABMD的面积,然后判定出④错误.
【解答】在菱形ABCD中,∵AB=BD,
∴AB=BD=AD,
∴△ABD是等边三角形,
∴根据菱形的性质可得∠BDF=∠C=60°,
∵BE=CF,
∴BC-BE=CD-CF,
即CE=DF,
在△BDF和△DCE中,CE=DF;∠BDF=∠C=60°;BD=CD,
∴△BDF≌△DCE(SAS),故①小题正确;
∴∠DBF=∠EDC,
∵∠DMF=∠DBF+∠BDE=∠EDC+∠BDE=∠BDC=60°,
∴∠BMD=180°-∠DMF=180°-60°=120°,故②小题正确;
∵∠DEB=∠EDC+∠C=∠EDC+60°,∠ABM=∠ABD+∠DBF=∠DBF+60°,
∴∠DEB=∠ABM,
又∵AD∥BC,
∴∠ADH=∠DEB,
∴∠ADH=∠ABM,
在△ABM和△ADH中,AB=AD;∠ADH=∠ABM;DH=BM,
∴△ABM≌△ADH(SAS),
∴AH=AM,∠BAM=∠DAH,
∴∠MAH=∠MAD+∠DAH=∠MAD+∠BAM=∠BAD=60°,
∴△AMH是等边三角形,故③小题正确;
∵△ABM≌△ADH,
∴△AMH的面积等于四边形ABMD的面积,
又∵△AMH的面积=![]() AM·
AM·![]() AM=
AM=![]() AM2,
AM2,
∴S四边形ABMD=![]() AM2,S四边形ABCD≠S四边形ABMD,故④小题错误,
AM2,S四边形ABCD≠S四边形ABMD,故④小题错误,
综上所述,正确的是①②③共3个.
故选C.
【点评】本题考查了菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质,题目较为复杂,特别是图形的识别有难度,从图形中准确确定出全等三角形并找出全等的条件是解题的关键.
科目:初中数学 来源: 题型:
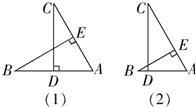 95、小明、小敏两人一起做数学作业,小敏把题读到如图(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说:“这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.
95、小明、小敏两人一起做数学作业,小敏把题读到如图(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说:“这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.科目:初中数学 来源: 题型:解答题
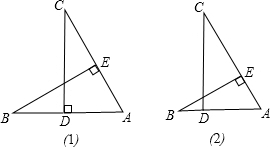 小明、小敏两人一起做数学作业,小敏把题读到如图(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说:“这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.
小明、小敏两人一起做数学作业,小敏把题读到如图(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说:“这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.科目:初中数学 来源:不详 题型:解答题

科目:初中数学 来源: 题型:
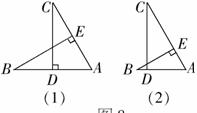
小明、小敏两人一起做数学作业,小敏把题读到如图(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说:“这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.
小明说:“小敏你错了,你未弄清本题的条件和结论,即使有CD⊥AB,BE⊥AC,公共角∠DAC=∠BAE,你的推理也是错误的.看我画的图(2),显然△DAC与△EAB是不全等的.再说本题不是要证明∠B=∠C,而是要证明BE=CD.”
(1)根据小敏所读的题,判断“∠B=∠C”对吗?她的推理对吗?若不对,请做出正确的推理.
(2)根据小明说的,要证明BE=CD,必然是小敏丢了题中条件,请你把小敏丢的条件找回来,并根据找出的条件,你做出判断BE=CD的正确推理.
(3)要判断三角形全等,从这个问题中你得到了什么启发?
科目:初中数学 来源: 题型:
科目:初中数学 来源:11.2 三角形全等的条件测试数学卷 题型:解答题
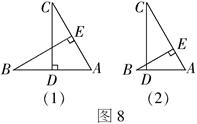
小明、小敏两人一起做数学作业,小敏把题读到如图8(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说: “这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.
小明说:“小敏你错了,你未弄清本题的条件和结论,即使有CD⊥AB,BE⊥AC,公共角∠DAC=∠BAE,你的推理也是错误的.看我画的图8(2),显然△DAC与△EAB是不全等的.再说本题不是要证明∠B=∠C,而是要证明BE=CD.”
【小题1】根据小敏所读的题,判断“∠B=∠C”对吗?她的推理对吗?若不对,请做出正确的推理.
【小题2】根据小明说的,要证明BE=CD,必然是小敏丢了题中条件,请你把小敏丢的条件找回来,并根据找出的条件,你做出判断BE=CD的正确推理.
【小题3】要判断三角形全等,从这个问题中你得到了什么启发?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com