
科目:初中数学 来源: 题型:


科目:初中数学 来源: 题型:解答题


科目:初中数学 来源:河北省期中题 题型:解答题


科目:初中数学 来源: 题型:
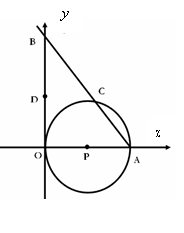
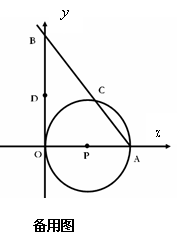
如图,⊙P与![]() 轴相切于坐标原点O(0,0),与
轴相切于坐标原点O(0,0),与![]() 轴相交于点A(5,0),过点A的直线AB与
轴相交于点A(5,0),过点A的直线AB与![]() 轴的正半轴交于点B,与⊙P交于点C.
轴的正半轴交于点B,与⊙P交于点C.
(1)已知AC=3,求点B的坐标;
(2)若AC=![]() , D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同一圆上,记这个圆的圆心为
, D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同一圆上,记这个圆的圆心为![]() ,函数
,函数![]() 的图象经过点
的图象经过点![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
科目:初中数学 来源: 题型:
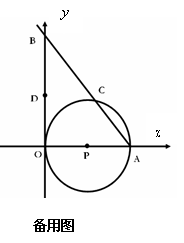
如图,⊙P与![]() 轴相切于坐标原点O(0,0),与
轴相切于坐标原点O(0,0),与![]() 轴相交于点A(5,0),过点A的直线AB与
轴相交于点A(5,0),过点A的直线AB与![]() 轴的正半轴交于点B,与⊙P交于点C.
轴的正半轴交于点B,与⊙P交于点C.
(1)已知AC=3,求点B的坐标;
(2)若AC=![]() , D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同一圆上,记这个圆的圆心为
, D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同一圆上,记这个圆的圆心为![]() ,函数
,函数![]() 的图象经过点
的图象经过点![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).

科目:初中数学 来源:2012届湖南省临武县楚江中学初中毕业学业考试数学试卷(带解析) 题型:解答题
如图,⊙P与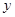 轴相切于坐标原点O(0,0),与
轴相切于坐标原点O(0,0),与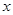 轴相交于点A(5,0),过点A的直线AB与
轴相交于点A(5,0),过点A的直线AB与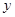 轴的正半轴交于点B,与⊙P交于点C.
轴的正半轴交于点B,与⊙P交于点C.
(1)已知AC=3,求点B的坐标;
(2)若AC=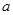 , D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同
, D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同
一圆上,记这个圆的圆心为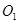 ,函数
,函数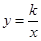 的图象经过点
的图象经过点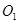 ,求
,求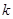 的值(用含
的值(用含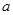 的代数式表示).
的代数式表示). 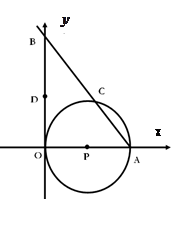
科目:初中数学 来源:不详 题型:解答题
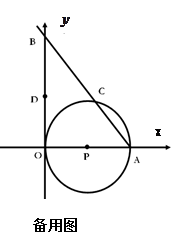
 轴相切于坐标原点O(0,0),与
轴相切于坐标原点O(0,0),与 轴相交于点A(5,0),过点A的直线AB与
轴相交于点A(5,0),过点A的直线AB与 轴的正半轴交于点B,与⊙P交于点C.
轴的正半轴交于点B,与⊙P交于点C. , D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同
, D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同 ,函数
,函数 的图象经过点
的图象经过点 ,求
,求 的值(用含
的值(用含 的代数式表示).
的代数式表示). 

科目:初中数学 来源: 题型:
 甲、乙从同一地点出发,甲乘坐电动观光车,乙步行,沿着同一条山路上山游玩,两人相约在电动车终点站会合.设乙出发x分钟后行走的路程为y米,图中的折线表示乙在整个行走过程中y与x的函数关系.甲乘坐的电动观光车平均速度为180米/分.
甲、乙从同一地点出发,甲乘坐电动观光车,乙步行,沿着同一条山路上山游玩,两人相约在电动车终点站会合.设乙出发x分钟后行走的路程为y米,图中的折线表示乙在整个行走过程中y与x的函数关系.甲乘坐的电动观光车平均速度为180米/分.科目:初中数学 来源:福建省期末题 题型:解答题

科目:初中数学 来源:不详 题型:解答题

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com