科目：初中数学 来源：1+1轻巧夺冠　同步讲解　九年级数学(下) 华东师大版 题型：044

如图，已知AC、BD交于O点，∠A＝∠D，AB＝DC，①请你写出符合条件的五个结论(对顶角相等除外，并且不要添加辅助线)．②从你写出的五个结论中，任选一个加以证明．

查看答案和解析>>

科目：初中数学 来源： 题型：

22、如图，在平行四边形ABCD纸片中，AC⊥AB，AC与BD相交于O，将纸△ABC沿对角线AC翻转180°，得到△AB′C，问以A、C、D、B′为顶点的四边形是什么形状的四边形？证明你的结论．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，在等边△ABC中，M、N分别是边AB，AC的中点，D为MN的中点，CD，BD的延长线分别交于AB，AC于点E，点F，下列结论正确的是（　　）
①MN的长是BC的

1

2

；
②△EMD的面积是△ABC面积的

1

16

；
③EM和FN的长度相等；
④图中全等的三角形有4对；
⑤连接EF，则四边形EBCF一定是等腰梯形．

A、①②⑤	B、①③④
C、①②④	D、①③⑤

查看答案和解析>>

科目：初中数学 来源： 题型：

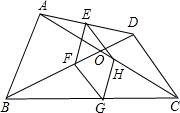如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD、BD、BC、AC的中点．
（1）求证：四边形EFGH是平行四边形；
（2）当四边形ABCD满足一个什么条件时，四边形EFGH是菱形？并证明你的结论．

查看答案和解析>>

科目：初中数学 来源： 题型：

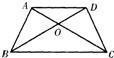17、如图，在等腰梯形ABCD中，AD∥BC，AC、BD相交于点O，有如下五个结论：
①△AOD∽△BOC；②∠DAC=∠DCA；③梯形ABCD是轴对称图形；④△AOB≌△AOD；⑤AC=BD．请把其中正确结论的序号填写在横线上

①③⑤

．

查看答案和解析>>

科目：初中数学 来源： 题型：

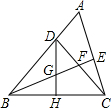如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，DH⊥BC于H，交BE于G，下列结论：①BD=CD；②AD+CF=BD；③CE=

1

2

BF；④AE=BG．其中正确的是（　　）

A、①②	B、①③
C、①②③	D、①②③④

查看答案和解析>>

科目：初中数学 来源： 题型：

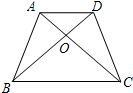20、如图，在等腰梯形ABCD中，AD∥BC，AB≠AD，对角线AC，BD相交于点O．如下四个结论：
①梯形ABCD是轴对称图形；
②∠DAC=∠DCA；
③△AOB全等于△DOC；
④△AOD相似于△BOC．请把其中正确结论的序号填在横线上：

134

．

查看答案和解析>>

科目：初中数学 来源： 题型：

6、如图，已知梯形ABCD中，AD∥BC，AB=CD=AD，AC、BD相交于O点，∠BCD=60°，下列结论中正确的有：①梯形ABCD是轴对称图形；②BC=2AD；③梯形ABCD是中心对称图形；④AC平分∠DCB．（　　）

A、①②

B、②③

C、①②④

D、②③④

查看答案和解析>>

科目：初中数学 来源： 题型：

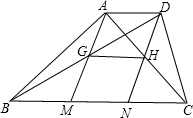如图，梯形ABCD中，AD∥BC，BC=3AD，M、N为底边BC的三等分点，连接AM，DN．
（1）求证：四边形AMND是平行四边形；
（2）连接BD、AC，AM与对角线BD交于点G，DN与对角线AC交于点H，且AC⊥BD．试判断四边形AGHD的形状，并证明你的结论．

查看答案和解析>>

科目：初中数学 来源： 题型：

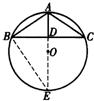16、如图，已知AB为⊙O的弦，M为AB的中点，P为⊙O上任意一点，以点P为圆心、2MO为半径作圆并交⊙O于点C、D，AC、BD交于点Q，请问：
（1）点Q是△PAB的什么“心”？
（2）点Q是否在⊙P上？试证明你的结论．
提示：（1）三角形的三条高线交于一点，称为垂心定理，此点称为垂心．
（2）三角形有内心、外心、重心、垂心等．

查看答案和解析>>