
科目:初中数学 来源: 题型:
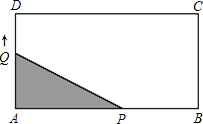 范围.
范围.科目:初中数学 来源: 题型:
 ,另一点停止运动.过点P作PE⊥CD于E,交DB于点F,连接AF、QF,设运动时间为t秒.
,另一点停止运动.过点P作PE⊥CD于E,交DB于点F,连接AF、QF,设运动时间为t秒.科目:初中数学 来源: 题型:
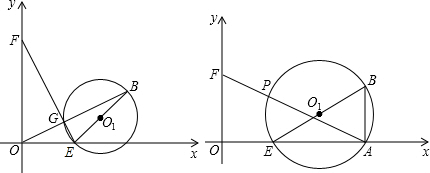
科目:初中数学 来源: 题型:
 值时有最大值,并求出最大值;若不存在,请说明理由.
值时有最大值,并求出最大值;若不存在,请说明理由.科目:初中数学 来源: 题型:
| 3 |
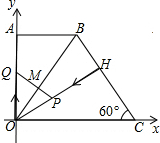 动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.
动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.科目:初中数学 来源: 题型:
| 3 | 5 |
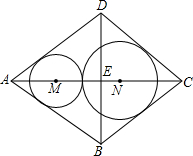 形零件(菱形铁片上只能加工同一直径的零件,不计加工过程中的损耗),问加工哪种零件能最充分地利用这种铁片并说明理由.
形零件(菱形铁片上只能加工同一直径的零件,不计加工过程中的损耗),问加工哪种零件能最充分地利用这种铁片并说明理由.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com