
科目:初中数学 来源:《24.4 中位线》2010年同步练习(解析版) 题型:选择题
科目:初中数学 来源:测试专家八年级数学下册 第19章 四边形、综合检测题 题型:013
以三角形的一条中位线和第三边上的中线为对角线的四边形是
A.梯形
B.平行四边形
C.菱形
D.矩形
科目:初中数学 来源: 题型:
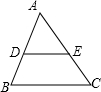 在八年级上册我们已经知道三角形的中位线具有如下性质:
在八年级上册我们已经知道三角形的中位线具有如下性质:| 1 | 2 |
科目:初中数学 来源: 题型:解答题
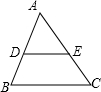 在八年级上册我们已经知道三角形的中位线具有如下性质:
在八年级上册我们已经知道三角形的中位线具有如下性质: BC;④DE∥BC.
BC;④DE∥BC.科目:初中数学 来源: 题型:解答题


 ,
, ,H(2c,0)(其中c>0).问当c为何值时,该抛物线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形?并求出所有符合条件的P点坐标.
,H(2c,0)(其中c>0).问当c为何值时,该抛物线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形?并求出所有符合条件的P点坐标.科目:初中数学 来源: 题型:
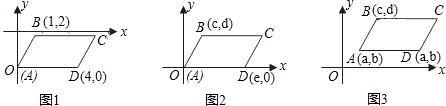
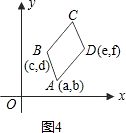
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com