
科目:初中数学 来源: 题型:
| PD-PH |
| PM |
| PD-PH |
| PM |

科目:初中数学 来源: 题型:解答题
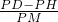 的值;
的值;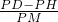 与x轴正半轴交点为S,点E、F是线段OS上的动点(不与点S重合),连接并延长DE,DF交⊙O于点B、C,直线BC交x轴于点G,若△DEF是以EF为底的等腰三角形,当E、F两点在OS上运动时(不与点S重合),∠OGC+∠DOG的值是否发生变化?若不变,请求出其值;若变化,请求出其变化范围.
与x轴正半轴交点为S,点E、F是线段OS上的动点(不与点S重合),连接并延长DE,DF交⊙O于点B、C,直线BC交x轴于点G,若△DEF是以EF为底的等腰三角形,当E、F两点在OS上运动时(不与点S重合),∠OGC+∠DOG的值是否发生变化?若不变,请求出其值;若变化,请求出其变化范围.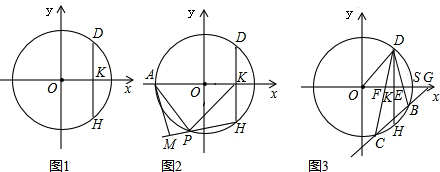
科目:初中数学 来源:不详 题型:单选题
| A.点P在⊙O内 | B.点P在⊙O上 | C.点P在⊙O外 | D.不能确定 |
科目:初中数学 来源:2011-2012学年江苏省苏州市立达中学九年级(上)期末数学试卷(解析版) 题型:选择题
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
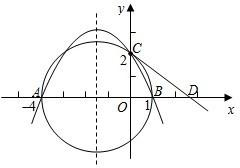 轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.
轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.科目:初中数学 来源: 题型:
 在平面直角坐标系中,抛物线经过O(0,0)、A(4,0)、E(3,-
在平面直角坐标系中,抛物线经过O(0,0)、A(4,0)、E(3,-2
| ||
| 3 |
科目:初中数学 来源: 题型:
| A、内含 | B、相交 | C、外切 | D、外离 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com