| 已知f(x)=ax3-3x+1对于x∈[-1,1]总有f(x)≥0 成立,则a=( ) |
相关习题
科目:高中数学
来源:
题型:
已知f(x)=ax3-3x+1对于x∈[-1,1]总有f(x)≥0 成立,则a=( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知f(x)=ax
3-3x+1对于x∈[-1,1]总有f(x)≥0 成立,则a=( )
查看答案和解析>>
科目:高中数学
来源:2009-2010学年福建省厦门六中高二(下)期中数学试卷(文科)(解析版)
题型:选择题
已知f(x)=ax3-3x+1对于x∈[-1,1]总有f(x)≥0 成立,则a=( )
A.a≥2
B.a≤4
C.a≥4
D.a=4
查看答案和解析>>
科目:高中数学
来源:2009-2010学年浙江省宁波市余姚中学高三(上)第一次质量检测数学试卷(理科)(解析版)
题型:选择题
已知f(x)=ax3-3x+1对于x∈[-1,1]总有f(x)≥0 成立,则a=( )
A.a≥2
B.a≤4
C.a≥4
D.a=4
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
已知f(x)=ax3-3x+1对于x∈[-1,1]总有f(x)≥0 成立,则a=
- A.
a≥2
- B.
a≤4
- C.
a≥4
- D.
a=4
查看答案和解析>>
科目:高中数学
来源:
题型:
已知三次函数f(x)=ax
3+bx
2+cx+d(a,b,c,d∈R)为奇函数,且在点(1,f(1))的切线方程为y=3x-2
(1)求函数f(x)的表达式.
(2)已知数列{a
n}的各项都是正数,且对于?n∈N
*,都有(
| n |
 |
| i=1 |
ai)
2=
| n |
 |
| i=1 |
f(ai),求数列{a
n}的首项a
1和通项公式.
(3)在(2)的条件下,若数列{b
n}满足b
n=4
n-m•2
an+1(m∈R,n∈N
*),求数列{b
n}的最小值.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省济宁市鱼台一中高二(下)期中数学试卷(文科)(解析版)
题型:解答题
已知三次函数f(x)=ax
3+bx
2+cx+d(a,b,c,d∈R)为奇函数,且在点(1,f(1))的切线方程为y=3x-2
(1)求函数f(x)的表达式.
(2)已知数列{a
n}的各项都是正数,且对于?n∈N
*,都有(

)
2=

,求数列{a
n}的首项a
1和通项公式.
(3)在(2)的条件下,若数列{b
n}满足b
n=4
n-m•2
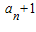
(m∈R,n∈N
*),求数列{b
n}的最小值.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年广东省执信中学高二(下)期中数学试卷(文科)(解析版)
题型:解答题
已知三次函数f(x)=ax
3+bx
2+cx+d(a,b,c,d∈R)为奇函数,且在点(1,f(1))的切线方程为y=3x-2
(1)求函数f(x)的表达式.
(2)已知数列{a
n}的各项都是正数,且对于?n∈N
*,都有(

)
2=

,求数列{a
n}的首项a
1和通项公式.
(3)在(2)的条件下,若数列{b
n}满足b
n=4
n-m•2

(m∈R,n∈N
*),求数列{b
n}的最小值.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年广东省珠海一中等六校高三(上)第二次联考数学试卷(文科)(解析版)
题型:解答题
已知三次函数f(x)=ax
3+bx
2+cx+d(a,b,c,d∈R)为奇函数,且在点(1,f(1))的切线方程为y=3x-2
(1)求函数f(x)的表达式.
(2)已知数列{a
n}的各项都是正数,且对于?n∈N
*,都有(

)
2=

,求数列{a
n}的首项a
1和通项公式.
(3)在(2)的条件下,若数列{b
n}满足b
n=4
n-m•2

(m∈R,n∈N
*),求数列{b
n}的最小值.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年广东省六校高三(上)第二次联考数学试卷(文科)(解析版)
题型:解答题
已知三次函数f(x)=ax
3+bx
2+cx+d(a,b,c,d∈R)为奇函数,且在点(1,f(1))的切线方程为y=3x-2
(1)求函数f(x)的表达式.
(2)已知数列{a
n}的各项都是正数,且对于?n∈N
*,都有(

)
2=

,求数列{a
n}的首项a
1和通项公式.
(3)在(2)的条件下,若数列{b
n}满足b
n=4
n-m•2

(m∈R,n∈N
*),求数列{b
n}的最小值.
查看答案和解析>>



 )2=
)2= ,求数列{an}的首项a1和通项公式.
,求数列{an}的首项a1和通项公式.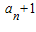 (m∈R,n∈N*),求数列{bn}的最小值.
(m∈R,n∈N*),求数列{bn}的最小值. )2=
)2= ,求数列{an}的首项a1和通项公式.
,求数列{an}的首项a1和通项公式. (m∈R,n∈N*),求数列{bn}的最小值.
(m∈R,n∈N*),求数列{bn}的最小值. )2=
)2= ,求数列{an}的首项a1和通项公式.
,求数列{an}的首项a1和通项公式. (m∈R,n∈N*),求数列{bn}的最小值.
(m∈R,n∈N*),求数列{bn}的最小值. )2=
)2= ,求数列{an}的首项a1和通项公式.
,求数列{an}的首项a1和通项公式. (m∈R,n∈N*),求数列{bn}的最小值.
(m∈R,n∈N*),求数列{bn}的最小值.