| 设a∈R,函数f(x)=ex+a?e-x的导函数是f′(x),且f′(x)是奇函数.若曲线y=f(x)的一条切线的斜率是,则切点的横坐标为( ) |
相关习题
科目:高中数学
来源:
题型:
设a∈R,函数f(x)=e
x+a•e
-x的导函数是f′(x),且f′(x)是奇函数.若曲线y=f(x)的一条切线的斜率是
,则切点的横坐标为( )
查看答案和解析>>
科目:高中数学
来源:
题型:
设a∈R,函数f(x)=e
x+a•e
-x的导函数y=f′(x)是奇函数,若曲线y=f(x)的一条切线斜率为
,则切点的横坐标为
ln2
ln2
.
查看答案和解析>>
科目:高中数学
来源:桂林模拟
题型:单选题
设a∈R,函数f(x)=e
x+a•e
-x的导函数是f′(x),且f′(x)是奇函数.若曲线y=f(x)的一条切线的斜率是
,则切点的横坐标为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设a∈R,函数f(x)=e
x+a•e
-x的导函数y=f′(x)是奇函数,若曲线y=f(x)的一条切线斜率为
,则切点的横坐标为______.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年辽宁省锦州市高二(下)期末数学试卷(理科)(解析版)
题型:选择题
设a∈R,函数f(x)=e
x+a•e
-x的导函数是f′(x),且f′(x)是奇函数.若曲线y=f(x)的一条切线的斜率是

,则切点的横坐标为( )
A.ln2
B.-ln2
C.

D.

查看答案和解析>>
科目:高中数学
来源:2009-2010学年黑龙江省哈尔滨六中高二(下)期末数学试卷(理科)(解析版)
题型:选择题
设a∈R,函数f(x)=e
x+a•e
-x的导函数是f′(x),且f′(x)是奇函数.若曲线y=f(x)的一条切线的斜率是

,则切点的横坐标为( )
A.ln2
B.-ln2
C.

D.

查看答案和解析>>
科目:高中数学
来源:2010-2011学年黑龙江省鹤岗一中高二(下)期中数学试卷(文科)(解析版)
题型:填空题
设a∈R,函数f(x)=e
x+a•e
-x的导函数y=f′(x)是奇函数,若曲线y=f(x)的一条切线斜率为

,则切点的横坐标为
.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年广西桂林十八中高三(上)第一次月考数学试卷(理科)(解析版)
题型:选择题
设a∈R,函数f(x)=e
x+a•e
-x的导函数是f′(x),且f′(x)是奇函数.若曲线y=f(x)的一条切线的斜率是

,则切点的横坐标为( )
A.ln2
B.-ln2
C.
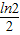
D.
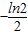
查看答案和解析>>
科目:高中数学
来源:2011-2012学年山东省德州市乐陵一中高三(上)期末数学复习训练试卷17(解析版)
题型:选择题
设a∈R,函数f(x)=e
x+a•e
-x的导函数是f′(x),且f′(x)是奇函数.若曲线y=f(x)的一条切线的斜率是

,则切点的横坐标为( )
A.ln2
B.-ln2
C.

D.

查看答案和解析>>
科目:高中数学
来源:2010-2011学年湖北省武汉市江汉区、黄冈市高三(上)期末数学试卷(理科)(解析版)
题型:选择题
设a∈R,函数f(x)=e
x+a•e
-x的导函数是f′(x),且f′(x)是奇函数.若曲线y=f(x)的一条切线的斜率是

,则切点的横坐标为( )
A.ln2
B.-ln2
C.

D.

查看答案和解析>>

 ,则切点的横坐标为( )
,则切点的横坐标为( )

 ,则切点的横坐标为( )
,则切点的横坐标为( )

 ,则切点的横坐标为 .
,则切点的横坐标为 . ,则切点的横坐标为( )
,则切点的横坐标为( )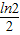
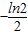
 ,则切点的横坐标为( )
,则切点的横坐标为( )

 ,则切点的横坐标为( )
,则切点的横坐标为( )
