若函数f(x)同时满足下列三个性质:
①最小正周期为π;
②图象关于直线x=对称;
③在区间[-,]上是增函数.
则y=f(x)的解析式可以是( )| A.y=sin(2x-) | B.y=sin(+) | C.y=cos(2x-) | D.y=cos(2x+) |
|
相关习题
科目:高中数学
来源:
题型:
若函数f(x)同时满足下列三个性质:
①最小正周期为π;
②图象关于直线x=
对称;
③在区间[-
,
]上是增函数.
则y=f(x)的解析式可以是( )
| A、y=sin(2x-) |
| B、y=sin(+) |
| C、y=cos(2x-) |
| D、y=cos(2x+) |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若函数f(x)同时满足下列三个性质:
①最小正周期为π;
②图象关于直线x=
对称;
③在区间[-
,
]上是增函数.
则y=f(x)的解析式可以是( )
| A.y=sin(2x-) | B.y=sin(+) | C.y=cos(2x-) | D.y=cos(2x+) |
查看答案和解析>>
科目:高中数学
来源:2011-2012学年江西省南昌二中高一(上)第二次月考数学试卷(解析版)
题型:选择题
若函数f(x)同时满足下列三个性质:
①最小正周期为π;
②图象关于直线x=
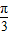
对称;
③在区间[-
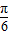
,
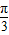
]上是增函数.
则y=f(x)的解析式可以是( )
A.y=sin(2x-
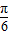
)
B.y=sin(

+

)
C.y=cos(2x-
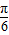
)
D.y=cos(2x+

)
查看答案和解析>>
科目:高中数学
来源:2012-2013学年内蒙古包头33中高一(下)期末数学试卷(文科)(解析版)
题型:选择题
若函数f(x)同时满足下列三个性质:
①最小正周期为π;
②图象关于直线x=
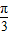
对称;
③在区间[-
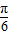
,
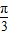
]上是增函数.
则y=f(x)的解析式可以是( )
A.y=sin(2x-
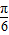
)
B.y=sin(
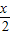
+

)
C.y=cos(2x-
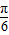
)
D.y=cos(2x+

)
查看答案和解析>>
科目:高中数学
来源:2011-2012学年江西省新余四中高一(上)段考数学试卷(三角函数1)(解析版)
题型:选择题
若函数f(x)同时满足下列三个性质:
①最小正周期为π;
②图象关于直线x=
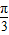
对称;
③在区间[-
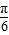
,
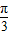
]上是增函数.
则y=f(x)的解析式可以是( )
A.y=sin(2x-

)
B.y=sin(

+

)
C.y=cos(2x-
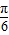
)
D.y=cos(2x+

)
查看答案和解析>>
科目:高中数学
来源:2011年高考数学复习:3.3 三角函数的图象和性质(1)(解析版)
题型:选择题
若函数f(x)同时满足下列三个性质:
①最小正周期为π;
②图象关于直线x=

对称;
③在区间[-

,
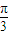
]上是增函数.
则y=f(x)的解析式可以是( )
A.y=sin(2x-

)
B.y=sin(
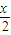
+
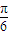
)
C.y=cos(2x-

)
D.y=cos(2x+
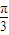
)
查看答案和解析>>
科目:高中数学
来源:2011年高考数学复习:3.3 三角函数的图象与性质(2)(解析版)
题型:选择题
若函数f(x)同时满足下列三个性质:
①最小正周期为π;
②图象关于直线x=

对称;
③在区间[-

,

]上是增函数.
则y=f(x)的解析式可以是( )
A.y=sin(2x-

)
B.y=sin(
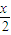
+
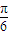
)
C.y=cos(2x-
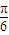
)
D.y=cos(2x+

)
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
若函数f(x)同时满足下列三个性质:
①最小正周期为π;
②图象关于直线x= 对称;
对称;
③在区间[- ,
, ]上是增函数.
]上是增函数.
则y=f(x)的解析式可以是
- A.
y=sin(2x-

)
- B.
y=sin(

+

)
- C.
y=cos(2x-

)
- D.
y=cos(2x+

)
查看答案和解析>>
科目:高中数学
来源:
题型:
若函数f(x)同时满足下列三个性质:①偶函数;②在区间(0,1)上是增函数;③有最小值,则y=f(x)的解析式可以是( )
| | | |
查看答案和解析>>
科目:高中数学
来源:2012-2013学年广东省清远一中高三(上)第二次月考数学试卷(理科)(解析版)
题型:选择题
若函数f(x)同时满足下列三个性质:①偶函数;②在区间(0,1)上是增函数;③有最小值,则y=f(x)的解析式可以是( )
A.y=e
x+e
-xB.y=1-x
2C.y=sin
D.

查看答案和解析>>

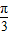 对称;
对称;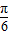 ,
,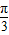 ]上是增函数.
]上是增函数.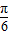 )
) +
+ )
)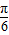 )
) )
)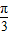 对称;
对称;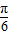 ,
,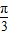 ]上是增函数.
]上是增函数.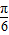 )
)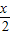 +
+ )
)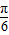 )
) )
)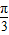 对称;
对称;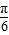 ,
,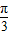 ]上是增函数.
]上是增函数. )
) +
+ )
)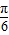 )
) )
) 对称;
对称; ,
,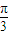 ]上是增函数.
]上是增函数. )
)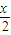 +
+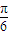 )
) )
) )
) 对称;
对称; ,
, ]上是增函数.
]上是增函数. )
) +
+ )
) )
) )
) 对称;
对称; ,
, ]上是增函数.
]上是增函数. )
) +
+ )
) )
) )
)