
等差数列{an}的前m项和Sm=100(m∈N且m≥2),则m(a2+am-1)=( )
|
科目:高中数学 来源:2008-2009学年北京市崇文区高一(下)期末数学试卷(解析版) 题型:选择题
科目:高中数学 来源: 题型:
| 用Sm表示S2m | S2m=2Sm+m2d | ||||
| 用Sm1、Sm2表示Sm1+m2 | Sm1+m2= Sm1+Sm2+m1m2d Sm1+Sm2+m1m2d ① | ||||
| 用Sm表示Snm | Snm= nSm+
nSm+ ②
|
科目:高中数学 来源: 题型:
(1)求{an}各项的和S;
(2)记{bn}的末项不大于![]() ,求{bn}项数的最值N;
,求{bn}项数的最值N;
(3)记{an}前n项和为Sn,{bn}前n项和为Tn,问是否存在自然数m,使Sm=Tn.
科目:高中数学 来源: 题型:
科目:高中数学 来源: 题型:
| S10 |
| 10 |
| S100 |
| 100 |
| S110 |
| 110 |
科目:高中数学 来源:不详 题型:填空题
| S10 |
| 10 |
| S100 |
| 100 |
| S110 |
| 110 |
科目:高中数学 来源:2010年上海市卢湾区高考数学一模试卷(文理合卷)(解析版) 题型:解答题
| 用Sm表示S2m | S2m=2Sm+m2d |
用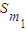 、 、 表示 表示 |  =______① =______① |
| 用Sm表示Snm | Snm=______② |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com