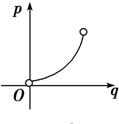
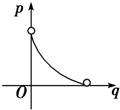
| 如图所示,已知圆x2+y2=4,过坐标原点但不与x轴重合的直线l、x轴的正半轴及圆围成了两个区域,它们的面积分别为p和q,则p关于q的函数图象的大致形状为图中的( ) |
相关习题
科目:高中数学
来源:
题型:
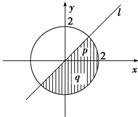
3、如图所示,已知圆x
2+y
2=4,过坐标原点但不与x轴重合的直线l、x轴的正半轴及圆围成了两个区域,它们的面积分别为p和q,则p关于q的函数图象的大致形状为图中的( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
如图所示,已知圆x
2+y
2=4,过坐标原点但不与x轴重合的直线l、x轴的正半轴及圆围成了两个区域,它们的面积分别为p和q,则p关于q的函数图象的大致形状为图中的( )
查看答案和解析>>
科目:高中数学
来源:2011年高三数学第一轮复习巩固与练习:函数的图象(解析版)
题型:选择题
如图所示,已知圆x
2+y
2=4,过坐标原点但不与x轴重合的直线l、x轴的正半轴及圆围成了两个区域,它们的面积分别为p和q,则p关于q的函数图象的大致形状为图中的( )
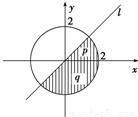
A.
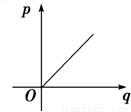
B.

C.

D.
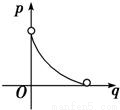
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
 如图所示,已知圆x2+y2=4,过坐标原点但不与x轴重合的直线l、x轴的正半轴及圆围成了两个区域,它们的面积分别为p和q,则p关于q的函数图象的大致形状为图中的
如图所示,已知圆x2+y2=4,过坐标原点但不与x轴重合的直线l、x轴的正半轴及圆围成了两个区域,它们的面积分别为p和q,则p关于q的函数图象的大致形状为图中的
- A.
- B.
- C.
- D.
查看答案和解析>>
科目:高中数学
来源:0103 期末题
题型:解答题
已知圆O:x
2+y
2=8交x轴于A,B两点,曲线C是以AB为长轴,直线

:x=-4为准线的椭圆。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若M是直线

上的任意一点,以OM为直径的圆K与圆O相交于P,Q两点,求证:直线PQ必过定点E,并求出点E的坐标;
(Ⅲ)如图所示,若直线PQ与椭圆C交于G,H两点,且
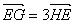
,试求此时弦PQ的长。
查看答案和解析>>
科目:高中数学
来源:2012-2013学年江苏省淮安市清江附中高三(上)第二次调研数学试卷(解析版)
题型:解答题
已知圆O:x
2+y
2=8交x轴于A,B两点,曲线C是以AB为长轴,直线l:x=-4为准线的椭圆.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若M是直线l上的任意一点,以OM为直径的圆K与圆O相交于P,Q两点,求证:直线PQ必过定点E,并求出点E的坐标;
(Ⅲ)如图所示,若直线PQ与椭圆C交于G,H两点,且

,试求此时弦PQ的长.

查看答案和解析>>
科目:高中数学
来源:2012-2013学年江苏省宿迁中学高三(上)第二次调研数学试卷(解析版)
题型:解答题
已知圆O:x
2+y
2=8交x轴于A,B两点,曲线C是以AB为长轴,直线l:x=-4为准线的椭圆.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若M是直线l上的任意一点,以OM为直径的圆K与圆O相交于P,Q两点,求证:直线PQ必过定点E,并求出点E的坐标;
(Ⅲ)如图所示,若直线PQ与椭圆C交于G,H两点,且

,试求此时弦PQ的长.

查看答案和解析>>
科目:高中数学
来源:2008-2009学年江苏省扬州市高三(上)期末数学试卷(解析版)
题型:解答题
已知圆O:x
2+y
2=8交x轴于A,B两点,曲线C是以AB为长轴,直线l:x=-4为准线的椭圆.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若M是直线l上的任意一点,以OM为直径的圆K与圆O相交于P,Q两点,求证:直线PQ必过定点E,并求出点E的坐标;
(Ⅲ)如图所示,若直线PQ与椭圆C交于G,H两点,且

,试求此时弦PQ的长.

查看答案和解析>>
科目:高中数学
来源:2012-2013学年江苏省淮安市清江附中高三(上)第二次调研数学试卷(解析版)
题型:解答题
已知圆O:x
2+y
2=8交x轴于A,B两点,曲线C是以AB为长轴,直线l:x=-4为准线的椭圆.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若M是直线l上的任意一点,以OM为直径的圆K与圆O相交于P,Q两点,求证:直线PQ必过定点E,并求出点E的坐标;
(Ⅲ)如图所示,若直线PQ与椭圆C交于G,H两点,且

,试求此时弦PQ的长.

查看答案和解析>>
科目:高中数学
来源:2012-2013学年江苏省宿迁中学高三(上)第二次调研数学试卷(解析版)
题型:解答题
已知圆O:x
2+y
2=8交x轴于A,B两点,曲线C是以AB为长轴,直线l:x=-4为准线的椭圆.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若M是直线l上的任意一点,以OM为直径的圆K与圆O相交于P,Q两点,求证:直线PQ必过定点E,并求出点E的坐标;
(Ⅲ)如图所示,若直线PQ与椭圆C交于G,H两点,且

,试求此时弦PQ的长.

查看答案和解析>>


 3、如图所示,已知圆x2+y2=4,过坐标原点但不与x轴重合的直线l、x轴的正半轴及圆围成了两个区域,它们的面积分别为p和q,则p关于q的函数图象的大致形状为图中的( )
3、如图所示,已知圆x2+y2=4,过坐标原点但不与x轴重合的直线l、x轴的正半轴及圆围成了两个区域,它们的面积分别为p和q,则p关于q的函数图象的大致形状为图中的( )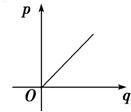
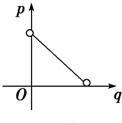
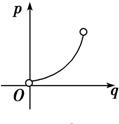
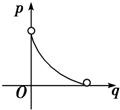
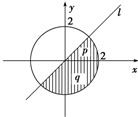





 如图所示,已知圆x2+y2=4,过坐标原点但不与x轴重合的直线l、x轴的正半轴及圆围成了两个区域,它们的面积分别为p和q,则p关于q的函数图象的大致形状为图中的
如图所示,已知圆x2+y2=4,过坐标原点但不与x轴重合的直线l、x轴的正半轴及圆围成了两个区域,它们的面积分别为p和q,则p关于q的函数图象的大致形状为图中的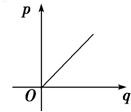
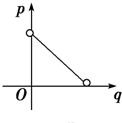
 :x=-4为准线的椭圆。
:x=-4为准线的椭圆。
 上的任意一点,以OM为直径的圆K与圆O相交于P,Q两点,求证:直线PQ必过定点E,并求出点E的坐标;
上的任意一点,以OM为直径的圆K与圆O相交于P,Q两点,求证:直线PQ必过定点E,并求出点E的坐标;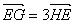 ,试求此时弦PQ的长。
,试求此时弦PQ的长。  ,试求此时弦PQ的长.
,试求此时弦PQ的长.
 ,试求此时弦PQ的长.
,试求此时弦PQ的长.
 ,试求此时弦PQ的长.
,试求此时弦PQ的长.
 ,试求此时弦PQ的长.
,试求此时弦PQ的长.
 ,试求此时弦PQ的长.
,试求此时弦PQ的长.