下列四个命题中正确的是( )| A.若a,b∈R,则|a|-|b|<|a+b| | | B.若a,b∈R,则|a-b|<|a|+|b| | | C.若实数a,b满足|a-b|=|a|+|b|,则ab≤0 | | D.若实数a,b满足|a|-|b|<|a+b|,则ab<0 |
|
相关习题
科目:高中数学
来源:《第3章 不等式》2010年单元测试卷(4)(解析版)
题型:选择题
下列四个命题中正确的是( )
A.若a,b∈R,则|a|-|b|<|a+b|
B.若a,b∈R,则|a-b|<|a|+|b|
C.若实数a,b满足|a-b|=|a|+|b|,则ab≤0
D.若实数a,b满足|a|-|b|<|a+b|,则ab<0
查看答案和解析>>
科目:高中数学
来源:2011年广东省广州市仲元中学高三数学专题训练:不等式(解析版)
题型:选择题
下列四个命题中正确的是( )
A.若a,b∈R,则|a|-|b|<|a+b|
B.若a,b∈R,则|a-b|<|a|+|b|
C.若实数a,b满足|a-b|=|a|+|b|,则ab≤0
D.若实数a,b满足|a|-|b|<|a+b|,则ab<0
查看答案和解析>>
科目:高中数学
来源:
题型:
下列四个命题中
①若a,b,c∈R,则“ac
2>bc
2”是“a>b”成立的充分不必要条件;
②当x∈(0,
)时,函数y=sinx+
的最小值为2;
③命题“若|x|>2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;
④函数f(x)=lnx+x-
在区间(1,2)上有且仅有一个零点.
其中正确命题的序号是
①④
①④
.
查看答案和解析>>
科目:高中数学
来源:
题型:
下列四个命题中,正确的命题的序号是
(1)
(1)
.
(1)若a,b,c∈R,ac
2>bc
2,则a>b;
(2)当x∈R时,sinx+cosx的最小值是2;
(3)两条直线互相垂直的充要条件是这两条直线的斜率乘积为-1
(4)设F
1、F
2为定点,P为平面上一动点,若|PF
1|+|PF
2|=2a( a>0),则动点P的轨迹为椭圆.
查看答案和解析>>
科目:高中数学
来源:2011-2012年山西省忻州一中高三(上)期中数学试卷(文科)(解析版)
题型:填空题
下列四个命题中
①若a,b,c∈R,则“ac
2>bc
2”是“a>b”成立的充分不必要条件;
②当x∈(0,
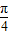
)时,函数y=sinx+

的最小值为2;
③命题“若|x|>2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;
④函数f(x)=lnx+x-

在区间(1,2)上有且仅有一个零点.
其中正确命题的序号是
.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年山西省忻州一中高三(上)期中数学试卷(理科)(解析版)
题型:填空题
下列四个命题中
①若a,b,c∈R,则“ac
2>bc
2”是“a>b”成立的充分不必要条件;
②当x∈(0,
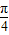
)时,函数y=sinx+

的最小值为2;
③命题“若|x|>2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;
④函数f(x)=lnx+x-

在区间(1,2)上有且仅有一个零点.
其中正确命题的序号是
.
查看答案和解析>>
科目:高中数学
来源:
题型:填空题
下列四个命题中
①若a,b,c∈R,则“ac2>bc2”是“a>b”成立的充分不必要条件;
②当x∈(0, )时,函数y=sinx+
)时,函数y=sinx+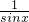 的最小值为2;
的最小值为2;
③命题“若|x|>2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;
④函数f(x)=lnx+x- 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点.
其中正确命题的序号是________.
查看答案和解析>>
科目:高中数学
来源:
题型:
7、下列四个结论中正确的个数为( )
①命题“若x2<1,则-1<x<1”的逆否命题是“若x>1或x<-1,则x2>1”
②已知p:?x∈R,sinx≤1,q:若a<b,则am2<bm2,则p∧q为真命题
③命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”
④复数z=a+bi(a,b∈R)表示纯虚数的充要条件是a=0.
查看答案和解析>>
科目:高中数学
来源:2008-2009学年湖南省永州市祁阳县陶铸中学等八校高二(上)联考数学试卷(理科)(解析版)
题型:选择题
在下列四个命题中
①已知A、B、C、D是空间的任意四点,则

.
②若{

}为空间的一组基底,则{

}也构成空间的一组基底.
③

.
④对于空间的任意一点O和不共线的三点A、B、C,若

(其中x,y,z∈R),则P、A、B、C四点共面.
其中正确的个数是( )
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学
来源:2009-2010学年浙江省宁波市海曙区效实中学高二(上)期末数学试卷(理科)(解析版)
题型:选择题
下列四个结论中正确的个数为( )
①命题“若x2<1,则-1<x<1”的逆否命题是“若x>1或x<-1,则x2>1”
②已知p:?x∈R,sinx≤1,q:若a<b,则am2<bm2,则p∧q为真命题
③命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”
④复数z=a+bi(a,b∈R)表示纯虚数的充要条件是a=0.
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>

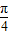 )时,函数y=sinx+
)时,函数y=sinx+ 的最小值为2;
的最小值为2; 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点.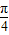 )时,函数y=sinx+
)时,函数y=sinx+ 的最小值为2;
的最小值为2; 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点. )时,函数y=sinx+
)时,函数y=sinx+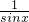 的最小值为2;
的最小值为2; 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点. .
. }为空间的一组基底,则{
}为空间的一组基底,则{ }也构成空间的一组基底.
}也构成空间的一组基底. .
. (其中x,y,z∈R),则P、A、B、C四点共面.
(其中x,y,z∈R),则P、A、B、C四点共面.