
科目:高中数学 来源:2012-2013学年福建省福州市文博中学高一(上)期中数学试卷(解析版) 题型:选择题
科目:高中数学 来源:2012-2013学年福建省厦门大学附属科技中学高一(上)期中数学试卷(解析版) 题型:选择题
科目:高中数学 来源: 题型:解答题
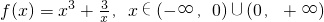 的最值中,
的最值中,| x | … | 0.1 | 0.2 | 0.5 | 0.7 | 0.9 | 1 | 1.1 | 1.2 | 1.3 | 2 | 3 | 4 | 5 | … |
| y | … | 30.00 | 15.01 | 6.13 | 4.63 | 4.06 | 4 | 4.06 | 4.23 | 4.50 | 9.50 | 28 | 64.75 | 125.6 | … |
科目:高中数学 来源:2012-2013学年福建省泉州市晋江市季延中学高一(上)期中数学试卷(解析版) 题型:解答题
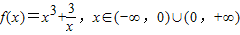 的最值中,
的最值中,| x | … | 0.1 | 0.2 | 0.5 | 0.7 | 0.9 | 1 | 1.1 | 1.2 | 1.3 | 2 | 3 | 4 | 5 | … |
| y | … | 30.00 | 15.01 | 6.13 | 4.63 | 4.06 | 4 | 4.06 | 4.23 | 4.50 | 9.50 | 28 | 64.75 | 125.6 | … |
科目:高中数学 来源:2011年四川省自贡市高考数学三模试卷(理科)(解析版) 题型:解答题
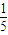 是函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为单调减函数的充要条件;
是函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为单调减函数的充要条件;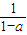 >1+a>
>1+a>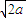 ;
;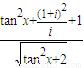 (x≠kπ+
(x≠kπ+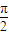 ),k∈Z,/为虚数单位)的最小值为2;
),k∈Z,/为虚数单位)的最小值为2;
科目:高中数学 来源: 题型:
 给出下列5个命题:
给出下列5个命题:| 1 |
| 5 |
| 1 |
| 1-a |
| 2a |
tan2x+
| ||
|
| π |
| 2 |
科目:高中数学 来源: 题型:
| 3 |
| x |
| x | … | 0.1 | 0.2 | 0.5 | 0.7 | 0.9 | 1 | 1.1 | 1.2 | 1.3 | 2 | 3 | 4 | 5 | … |
| y | … | 30.00 | 15.01 | 6.13 | 4.63 | 4.06 | 4 | 4.06 | 4.23 | 4.50 | 9.50 | 28 | 64.75 | 125.6 | … |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com