练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    直线l的斜率是直线x+2y+3=0的斜率的2倍，且过点（1，2），则直线l的方程为（　　）
    A．y=-4x+6B．y=-4x+4C．y=-x+3D．y=-4x-4
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    直线l的斜率是直线x+2y+3=0的斜率的2倍，且过点（1，2），则直线l的方程为（　　）
    A、y=-4x+6B、y=-4x+4C、y=-x+3D、y=-4x-4

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    直线l的斜率是直线x+2y+3=0的斜率的2倍，且过点（1，2），则直线l的方程为（　　）
    A．y=-4x+6B．y=-4x+4C．y=-x+3D．y=-4x-4

    查看答案和解析>>

    科目：高中数学 来源：《第2章 直线与方程》2011年单元测试卷（解析版） 题型：选择题

    直线l的斜率是直线x+2y+3=0的斜率的2倍，且过点（1，2），则直线l的方程为（ ）
    A．y=-4x+6
    B．y=-4x+4
    C．y=-x+3
    D．y=-4x-4

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    直线l的斜率是直线x+2y+3=0的斜率的2倍，且过点（1，2），则直线l的方程为


    1. A.
      y=-4x+6
    2. B.
      y=-4x+4
    3. C.
      y=-x+3
    4. D.
      y=-4x-4

    查看答案和解析>>

    科目：高中数学 来源：天骄之路中学系列　读想用　高二数学(上) 题型：044

    若直线l满足如下条件，分别求出其方程．

    (1)斜率为，且与两坐标轴围成的三角形面积为6；

    (2)经过两点A(1，0)及B(m，1)；

    (3)将直线l绕其上一点P沿顺时针方向旋转角α(0°＜α＜90°)所得直线方程是x－y－2＝0，若继续旋转90°－α，所得直线方程为x＋2y＋1＝0；

    (4)过点(－a，0)，(a＞0)且割第二象限得一面积为S的三角形区域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知中心在原点的双曲线C的一个焦点是F1(-3,0),一条渐近线的方程是x-2y=0.

    (1)求双曲线C的方程;

    (2)若以k(k≠0)为斜率的直线l与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为,求k的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知中心在原点的双曲线C的一个焦点是F1(-3,0),一条渐近线的方程是x-2y=0.

    (1)求双曲线C的方程;

    (2)若以k(k≠0)为斜率的直线l与双曲线C相交于两个不同的点M,N且线段MN的垂直平分线与两坐标轴围成的三角形的面积为,求k的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：云南省昆明一中2012届高三第三次月测数学理科试题（人教版） 题型：044

    已知双曲线(a＞0，b＞0)的一个焦点坐标是(3，0)，一条渐近线方程是

    x＋2y＝0．

    (Ⅰ)求双曲线的方程；

    (Ⅱ)若斜率为k(k≠0)的直线l与该双曲线相交于不同的两点M、N，且线段MN的垂直平分线与两坐标轴围成的三角形面积为，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    点P的横坐标和纵坐标分别是函数(x＜0)取得最大值时的x、y值，又直线l过直线x－2y＋3=0和x＋2y－9=0的交点，且斜率为，则点P到直线l的距离为

    [　　]

    A．4

    B．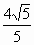

    C．14

    D．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：013

    点P的横坐标和纵坐标分别是函数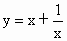(x＜0)取得最大值时的x、y值，又直线l过直线x－2y＋3=0和x＋2y－9=0的交点，且斜率为，则点P到直线l的距离为

    [　　]

    A．4
    B．
    C．14
    D．

    查看答案和解析>>


    同步练习册答案