练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在极坐标系中，当a＞0时，直线ρcosθ=a截曲线ρ=2acosθ所得弦长是（　　）
    A．
    a
    2
    		B．aC．2aD．4a
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    在极坐标系中，当a＞0时，直线ρcosθ=a截曲线ρ=2acosθ所得弦长是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    在极坐标系中，当a＞0时，直线ρcosθ=a截曲线ρ=2acosθ所得弦长是（　　）
    A．
    a
    2
    		B．aC．2aD．4a

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年北京市昌平区高二（下）期末数学试卷（理科）（解析版） 题型：选择题

    在极坐标系中，当a＞0时，直线ρcosθ=a截曲线ρ=2acosθ所得弦长是（ ）
    A．
    B．a
    C．2a
    D．4a

    查看答案和解析>>

    科目：高中数学 来源：2012年河南省洛阳市高考数学二模试卷（文科）（解析版） 题型：解答题

    选修4-4：坐标系与参数方程
    在直角坐标系xOy中，曲线C1的参数方程为（α为参数），直线l的参数方程为（t为参数）．以原点O为极点，以x轴非负半轴为极轴，与直角坐标系xOy取相同的长度单位，建立极坐标系．设曲线C2的极坐标方程为ρ=asinθ（a＞0）．
    （1）当直线l与曲线C2相切时求a的值；
    （2）求直线l被曲线C1所截得的弦长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•石家庄二模）选修4-4：坐标系与参数方程
    在平面直角坐标系xOy中，以原点0为极点，x轴的正半轴为极轴，建立极坐标系，已知圆C的极坐标方程为ρ=2acos（θ+
    π
    4
    ）（a＞0）．
    （Ⅰ）当a=2
    		2
    时，设OA为圆C的直径，求点A的直角坐标；
    （Ⅱ）直线l的参数方程是
    x=2t
    y=4t
    （t为参数），直线l被圆C截得的弦长为d，若d≥
    		2
    ，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：解答题

    在平面直角坐标系xOy中，曲线C1的参数方程为（φ为参数），曲线C2的参数方程为（a＞b＞0，φ为参数）在以O为极点，x轴的正半轴为极轴的极坐标系中，射线l：θ=α与C1，C2各有一个交点．当α=0时，这两个交点间的距离为2，当α=时，这两个交点重合．
    （I）分别说明C1，C2是什么曲线，并求出a与b的值；
    （II）设当α=时，l与C1，C2的交点分别为A1，B1，当α=﹣时，l与C1，C2的交点为A2，B2，求四边形A1A2B2B1的面积．

    查看答案和解析>>

    科目：高中数学 来源：《第1讲 坐标系》、《第2讲 参数方程》2011年单元测试卷（骆驼坳中学）（解析版） 题型：解答题

    在平面直角坐标系xOy中，曲线C1的参数方程为（φ为参数），曲线C2的参数方程为（a＞b＞0，φ为参数）在以O为极点，x轴的正半轴为极轴的极坐标系中，射线l：θ=α与C1，C2各有一个交点．当α=0时，这两个交点间的距离为2，当α=时，这两个交点重合．
    （I）分别说明C1，C2是什么曲线，并求出a与b的值；
    （II）设当α=时，l与C1，C2的交点分别为A1，B1，当α=-时，l与C1，C2的交点为A2，B2，求四边形A1A2B2B1的面积．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河南省新乡市卫辉一中高三（下）3月月考数学试卷（理科）（解析版） 题型：解答题

    在平面直角坐标系xOy中，曲线C1的参数方程为（φ为参数），曲线C2的参数方程为（a＞b＞0，φ为参数）在以O为极点，x轴的正半轴为极轴的极坐标系中，射线l：θ=α与C1，C2各有一个交点．当α=0时，这两个交点间的距离为2，当α=时，这两个交点重合．
    （I）分别说明C1，C2是什么曲线，并求出a与b的值；
    （II）设当α=时，l与C1，C2的交点分别为A1，B1，当α=-时，l与C1，C2的交点为A2，B2，求四边形A1A2B2B1的面积．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河南省新乡市卫辉一中高三（下）3月月考数学试卷（文科）（解析版） 题型：解答题

    在平面直角坐标系xOy中，曲线C1的参数方程为（φ为参数），曲线C2的参数方程为（a＞b＞0，φ为参数）在以O为极点，x轴的正半轴为极轴的极坐标系中，射线l：θ=α与C1，C2各有一个交点．当α=0时，这两个交点间的距离为2，当α=时，这两个交点重合．
    （I）分别说明C1，C2是什么曲线，并求出a与b的值；
    （II）设当α=时，l与C1，C2的交点分别为A1，B1，当α=-时，l与C1，C2的交点为A2，B2，求四边形A1A2B2B1的面积．

    查看答案和解析>>

    科目：高中数学 来源：2011年辽宁省高考数学试卷（理科）（解析版） 题型：解答题

    在平面直角坐标系xOy中，曲线C1的参数方程为（φ为参数），曲线C2的参数方程为（a＞b＞0，φ为参数）在以O为极点，x轴的正半轴为极轴的极坐标系中，射线l：θ=α与C1，C2各有一个交点．当α=0时，这两个交点间的距离为2，当α=时，这两个交点重合．
    （I）分别说明C1，C2是什么曲线，并求出a与b的值；
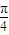    （II）设当α=时，l与C1，C2的交点分别为A1，B1，当α=-时，l与C1，C2的交点为A2，B2，求四边形A1A2B2B1的面积．

    查看答案和解析>>


    同步练习册答案