
在数轴上从左至右的三个数为a,1+a,-a,则a的取值范围是( )
|
科目:初中数学 来源:2012年苏教版初中数学八年级下7.6一元一次不等式组练习卷(解析版) 题型:选择题
在数轴上从左至右的三个数为a,1+a,-a,则a的取值范围是( )
A、a< B、a<0 C、a>0 D、a<-
B、a<0 C、a>0 D、a<-
科目:初中数学 来源:湖北省中考真题 题型:解答题
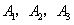 是抛物线
是抛物线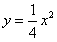 图象上的三点,若
图象上的三点,若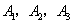 三点的横坐标从左至右依次为1,2,3.求
三点的横坐标从左至右依次为1,2,3.求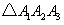 的面积.
的面积.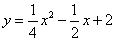 和
和 ,其他条件不变,请分别直接写出两种情况下
,其他条件不变,请分别直接写出两种情况下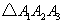 的面积.
的面积.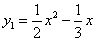 ;
; ;
;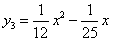 ;
;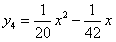 ;
; ;依据变化规律,请你写出抛物线组第n个式子
;依据变化规律,请你写出抛物线组第n个式子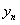 的函数解析式;现在x轴上有三点
的函数解析式;现在x轴上有三点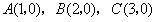 .经过
.经过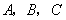 向x轴作垂线,分别交抛物线组
向x轴作垂线,分别交抛物线组 于
于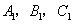 ;
;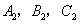 ;
; ;…;
;…;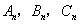 .记
.记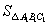 为
为 ,
,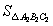 为
为 ,…,
,…, 为
为 ,试求
,试求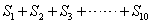 的值.
的值. 时有
时有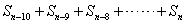 的值不小于
的值不小于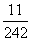 ,请探求此条件下正整数
,请探求此条件下正整数 是否存在最大值,若存在,请求出此值;若不存在,请说明理由.
是否存在最大值,若存在,请求出此值;若不存在,请说明理由.
科目:初中数学 来源: 题型:解答题
如图,已知抛物线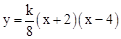 (
(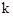 为常数,且
为常数,且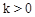 )与
)与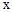 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与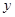 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线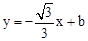 与抛物线的另一交点为D.
与抛物线的另一交点为D.
(1)若点D的横坐标为-5,求抛物线的函数表达式;
(2)若在第一象限的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求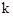 的值;
的值;
(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止. 当点F的坐标是多少时,点M在整个运动过程中用时最少?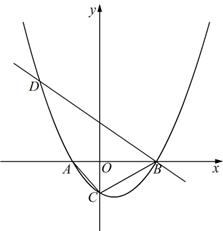
科目:初中数学 来源:不详 题型:解答题
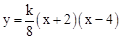 (
(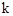 为常数,且
为常数,且 )与
)与 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线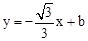 与抛物线的另一交点为D.
与抛物线的另一交点为D.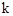 的值;
的值;
科目:初中数学 来源: 题型:
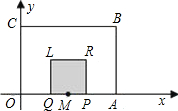 Q为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与矩形OABC重叠部分(阴影部分)的面积为S(平方单位).
Q为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与矩形OABC重叠部分(阴影部分)的面积为S(平方单位).科目:初中数学 来源: 题型:解答题
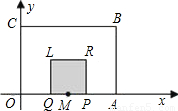
 Q为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与矩形OABC重叠部分(阴影部分)的面积为S(平方单位).
Q为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与矩形OABC重叠部分(阴影部分)的面积为S(平方单位).科目:初中数学 来源:2011年第2届“珥中杯”数学竞赛试卷(初三)(解析版) 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com