
设y=kx+b,当x=1时,y=1:当x=2时,y=4,那么( )
|
科目:初中数学 来源:不详 题型:单选题
| A.k=3,b=-2 | B.k=-2,b=3 | C.k=-3,b=2 | D.k=-3,b=-2 |
科目:初中数学 来源: 题型:
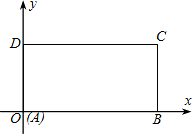 如图,在平面直角坐标系xoy中,已知矩形ABCD的边AB、AD分别在x轴、y轴上,点A与坐标原点重合,且AB=2,AD=1.
如图,在平面直角坐标系xoy中,已知矩形ABCD的边AB、AD分别在x轴、y轴上,点A与坐标原点重合,且AB=2,AD=1.科目:初中数学 来源: 题型:解答题
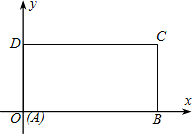 如图,在平面直角坐标系xoy中,已知矩形ABCD的边AB、AD分别在x轴、y轴上,点A与坐标原点重合,且AB=2,AD=1.
如图,在平面直角坐标系xoy中,已知矩形ABCD的边AB、AD分别在x轴、y轴上,点A与坐标原点重合,且AB=2,AD=1.科目:初中数学 来源:第25章《图形的变换》中考题集(29):25.3 轴对称变换(解析版) 题型:解答题

科目:初中数学 来源:2007年全国中考数学试题汇编《图形的对称》(03)(解析版) 题型:解答题

科目:初中数学 来源:2007年全国中考数学试题汇编《一次函数》(06)(解析版) 题型:解答题

科目:初中数学 来源:2007年湖北省咸宁市中考数学试卷(解析版) 题型:解答题

科目:初中数学 来源: 题型:解答题
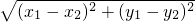 .例如:若
.例如:若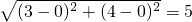 .
.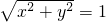 ,即x2+y2=1成立;反过来,如果点P(x,y)的坐标满足等式x2+y2=1,那么点P必在⊙O上,这时,我们就把等式x2+y2=1称为⊙O的方程.
,即x2+y2=1成立;反过来,如果点P(x,y)的坐标满足等式x2+y2=1,那么点P必在⊙O上,这时,我们就把等式x2+y2=1称为⊙O的方程.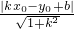 .
.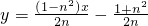 的距离.
的距离.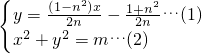 ,其中n≠0,m>0.
,其中n≠0,m>0.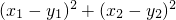 是与n无关的常数,并求出这个常数.
是与n无关的常数,并求出这个常数.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com