如果a，b都是不为零的有理数，且|a|-b=0，则a，b的关系是（　　）

A．a=b

B．a=|b|

C．a=±b

D．以上都不对

相关习题

科目：初中数学 来源： 题型：

如果a，b都是不为零的有理数，且|a|-b=0，则a，b的关系是（　　）

A．a=b

B．a=|b|

C．a=±b

D．以上都不对

科目：初中数学 来源：不详 题型：单选题

如果a，b都是不为零的有理数，且|a|-b=0，则a，b的关系是（　　）

A．a=b

B．a=|b|

C．a=±b

D．以上都不对

科目：初中数学 来源： 题型：单选题

如果a，b都是不为零的有理数，且|a|-b=0，则a，b的关系是

科目：初中数学 来源：中学教材全解　七年级数学下　(北京师大版) 北京师大版 题型：044

小明的爸爸在午饭过后，突然心血来潮，欲前往投注站买六合彩．小明却从裤袋里拿出一枚硬币，一脸认真地对爸爸说：“你真的甘愿把钱投注在一个中奖机会近似为零的游戏中吗？不如你试用这个硬币去测试一下今天的运气吧．

如果连续24次掷得硬币的同一面(正面或背面皆可)朝上，你再去投注也未迟呢！”

拿过小明的硬币投掷数次后，爸爸说：“不可能都同一面朝上，这与买彩票有什么关系？我还是去买彩票．”小明说：“这里面有科学道理，可以让我给你算一算中奖的机会有多大，之后，你再去买也不迟．”

小明利用了概率计算的乘法定律：若P₁和P₂分别为事件E₁和E₂出现的概率，则E₁和E₂同时出现的概率或E₂跟随E₁出现的概率为P₁×P₂．这一种运算方式可推广到n个事件出现的情况．

小明拿出纸与计算器，把六合彩中一等奖、二等奖、三等奖的概率逐一进行下面的运算：

中一等奖者，需从47个号码中选中6个与开采出来相同的号码；二等奖则须中5个号码和1个特别号码；若只中5个号码，便会得三等奖．基于这些中奖的条件，小明利用概率的乘法定律计算出以下的概率．

中一等奖的概率＝＝0.000 000 09(精确至8位小数)．

中二等奖的概率＝＝0.000 000 6(精确至7位小数)．

中三等奖的概率＝＝0.000 02(精确至5位小数)．

计算后，小明说中六合彩的机会可以说近似为0，爸爸说：“你为什么让我连续掷硬币呢？它与中六合彩有联系吗？”小明告诉爸爸连续24次掷硬币且同一面朝上的概率为是一个近似于零的数与中六合彩的概率可以相比．看了小明的计算，爸爸打消了买六合彩中奖的念头．

科目：初中数学 来源： 题型：解答题

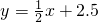血橙一果肉酷似鲜血的颜色而得名，它本质上属脐橙类，现在已经开发出多种品种，果实一般在1月下旬成熟．由于果农在生产实践中积累了丰富的管理经验，大多采取了留树保鲜技术措施，将鲜果供应期拉长到了5月初．重庆市万州区晚熟柑橘一血橙为主，其中沙河街孙家村是万州血橙老产区，主要销售市场是成都、重庆市区、万州城区，据以往经验，孙家村上半年1-5月血橙的售价y（元/千克）与月份x之间满足一次函数关系 $数学公式$ （1≤x≤5，且x是整数）．其销售量P（千克）与月份之间的相关数据如下表：
月份x 1月 2月 3月 4月 5月
销售量P（千克） 70000 65000 60000 55000 50000
（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，求月销售量P（千克）与月份x之间的函数关系式；
（2）血橙在上半年1-5月的哪个月出售，可使销售金额W（元）最大？最大金额是多少元？；
（3）由于气候适宜以及保鲜技术的提高，预计该产区今年5月将收获60000千克的血橙，并按（2）问中的获得最大销售金额时的销售量售出新鲜血橙．剩下的血橙的果肉与石榴、白糖按5：2：1的比例制成“石榴•血橙白茶果冻”出售（以下简称“果冻”，制作过程中的损耗忽略不计），已知平均每千克的血橙含0.8千克的果肉．产区生产商最初将每千克果冻的批发价定位26元，超市的零售价比批发价高a%，当销售了这批果冻的四分之三后，考虑到制作和营运成本的提高，生产商将批发价提高了a%，超市的零售价也跟着在此批发价的基础上提高了a%，最后该产区将这批果冻在超市全部出售后的销售总额达到了390000．求a的值．（结果保留整数）
（参考数据：10.52²≈110.67，10.53²≈110.88，10.54²≈111.09，10.55²≈111.30）

同步练习册答案

月份x	1月	2月	3月	4月	5月
销售量P（千克）	70000	65000	60000	55000	50000