练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    设a、b为正整数（a＞b），p是a、b的最大公约数，q是a、b的最小公倍数，则p，q，a，b的大小关系是（　　）
    A．p≥q≥a＞bB．q≥a＞b≥pC．q≥p≥a＞bD．p≥a＞b≥q
    B
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源：广东省中考真题 题型：解答题

    如图，在平面直角坐标系xoy中，已知抛物线经过点A（0，4），B（1，0），C（5，0），抛物线对称轴l与x轴相交于点M。
    （1）求抛物线的解析式和对称轴；
    （2）设点P为抛物线（x＞5）上的一点，若以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数，请你直接写出点P的坐标；
    （3）连接AC，探索：在直线AC下方的抛物线上是否存在一点N，使△NAC的面积最大？若存在，请你求出点N的坐标；若不存在，请你说明理由。

    查看答案和解析>>

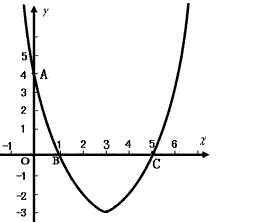
    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系xoy中，已知抛物线经过点A（0，4），B（1，0），C（5，0），抛物线对称轴l与x轴相交于点M．
    （1）求抛物线的解析式和对称轴；
    （2）设点P为抛物线（x＞5）上的一点，若以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数，请你直接写出点P的坐标；
    （3）连接AC．探索：在直线AC下方的抛物线上是否存在一点N，使△NAC的面积最大？若存在，请你求出点N的坐标；若不存在，请你说明理由．

    查看答案和解析>>

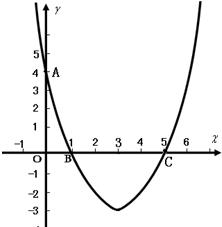
    科目：初中数学 来源：2012年贵州省黔西南州中考数学试卷（解析版） 题型：解答题

    如图，在平面直角坐标系xOy中，已知抛物线经过点A（0，4），B（1，0），C（5，0），抛物线的对称轴l与x轴相交于点M．
    （1）求抛物线对应的函数解析式和对称轴；
    （2）设点P为抛物线（x＞5）上的一点，若以A、O、M、P为顶点的四边形的四条边的长度为四个连续的正整数，请你直接写出点P的坐标；
    （3）连接AC，探索：在直线AC下方的抛物线上是否存在一点N，使△NAC的面积最大？若存在，请你求出点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

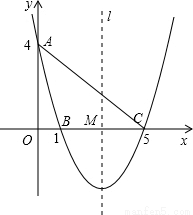
    科目：初中数学 来源： 题型：

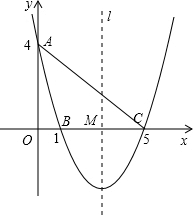    （2012•黔西南州）如图，在平面直角坐标系xOy中，已知抛物线经过点A（0，4），B（1，0），C（5，0），抛物线的对称轴l与x轴相交于点M．
    （1）求抛物线对应的函数解析式和对称轴；
    （2）设点P为抛物线（x＞5）上的一点，若以A、O、M、P为顶点的四边形的四条边的长度为四个连续的正整数，请你直接写出点P的坐标；
    （3）连接AC，探索：在直线AC下方的抛物线上是否存在一点N，使△NAC的面积最大？若存在，请你求出点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    设a、b为正整数（a＞b），p是a、b的最大公约数，q是a、b的最小公倍数，则p，q，a，b的大小关系是（　　）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    设a、b为正整数（a＞b），p是a、b的最大公约数，q是a、b的最小公倍数，则p，q，a，b的大小关系是（　　）
    A．p≥q≥a＞bB．q≥a＞b≥pC．q≥p≥a＞bD．p≥a＞b≥q

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，点P在AB上，AP=2.点E、F同时从点P出发，分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动，点E到达点A后立即以原速度沿AB向点B运动，点F运动到点B时停止，点E也随之停止.在点E、F运动过程中，以EF为边作正方形EFGH，使它与△ABC在线段AB的同侧，设E、F运动的时间为t秒（t＞0），正方形EFGH与△ABC重叠部分面积为S.

    1.当t=1时，正方形EFGH的边长是            ；

    当t=3时，正方形EFGH的边长是            ；

    2.当0＜t≤2时，求S与t的函数关系式；

    3. 直接答出：在整个运动过程中，当t为何值时，S最大？最大面积是多少？

     

    查看答案和解析>>

    科目：初中数学 来源：2012届江苏省淮安市涟水县九年级中考模拟（一）数学试卷（带解析） 题型：解答题

    如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，点P在AB上，AP=2.点E、F同时从点P出发，分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动，点E到达点A后立即以原速度沿AB向点B运动，点F运动到点B时停止，点E也随之停止.在点E、F运动过程中，以EF为边作正方形EFGH，使它与△ABC在线段AB的同侧，设E、F运动的时间为t秒（t＞0），正方形EFGH与△ABC重叠部分面积为S.
    【小题1】当t=1时，正方形EFGH的边长是            ；
    当t=3时，正方形EFGH的边长是            ；
    【小题2】当0＜t≤2时，求S与t的函数关系式；
    【小题3】直接答出：在整个运动过程中，当t为何值时，S最大？最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年江苏省淮安市涟水县九年级中考模拟（一）数学试卷（解析版） 题型：解答题

    如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，点P在AB上，AP=2.点E、F同时从点P出发，分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动，点E到达点A后立即以原速度沿AB向点B运动，点F运动到点B时停止，点E也随之停止.在点E、F运动过程中，以EF为边作正方形EFGH，使它与△ABC在线段AB的同侧，设E、F运动的时间为t秒（t＞0），正方形EFGH与△ABC重叠部分面积为S.[来源:Zxxk.Com]

    1.当t=1时，正方形EFGH的边长是             ；

    当t=3时，正方形EFGH的边长是             ；

    2.当0＜t≤2时，求S与t的函数关系式；

    3. 直接答出：在整个运动过程中，当t为何值时，S最大？最大面积是多少？

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，点P在AB上，AP=2，点E、F同时从点P出发，分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动，点E到达点A后立刻以原速度沿AB向点B运动，点F运动到点B时停止，点E也随之停止．在点E、F运动过程中，以EF为边作正方形EFGH，使它与△ABC在线段AB的同侧．设E、F运动的时间为精英家教网t/秒（t＞0），正方形EFGH与△ABC重叠部分面积为S．
    （1）当t=1时，正方形EFGH的边长是
     
    ．当t=3时，正方形EFGH的边长是
     
    ．
    （2）当0＜t≤2时，求S与t的函数关系式；
    （3）直接答出：在整个运动过程中，当t为何值时，S最大？最大面积是多少？

    查看答案和解析>>


    同步练习册答案