已知：抛物线与轴的一个交点为．

(1)求抛物线与轴的另一个交点的坐标；

(2)是抛物线与轴的交点，是抛物线上的一点，且以为一底的梯形的面积为9，求此抛物线的解析式；

(3)是第二象限内到轴、轴的距离的比为5：2的点，如果点E在(2)中的抛物线上，且它与点A在此抛物线对称轴的同侧．问：在抛物线的对称轴上，是否存在点P，使朋的周长最小?若存在，求出点P的坐标；若不存在，请说明理由．

若点P在第二象限内，且到x轴、y轴的距离分别为3和4，则点P的坐标为

1. A.
   （-4，3）
2. B.
   （4，-3）
3. C.
   （3，-4）
4. D.
   （-3，4）

　　(1)求抛物线与x轴的另一个交点B的坐标；

　　(2)D是抛物线与y轴的交点，C是抛物线上的一点，且以AB为一底的梯形ABCD的面积为9，求此抛物线的解析式；

　　(3)E是第二象限内到x轴、y轴的距离的比为5：2的点，如果点E在(2)中的抛物线上，且它与点A在此抛物线对称轴的同侧，问：在抛物线的对称轴上是否存在点P，使ΔAPE的周长最小？若存在，求出点P的坐标；若不存在，请说明理由．

(2004山东泰安)若点P在第二象限内，且到x轴、y轴的距离分别为3和4，则点P的坐标为

[　　]

如图，平行四边形ABCD在平面直角坐标系中，AD=6，若OA、OB的长是关于x的一元二次方程的两个根，且。

（1）则点C的坐标是_____________，点D的坐标是__________；

（2）若将此平行四边形ABCD沿x轴正方向向右平移3个单位，沿y轴正方向向上平移2个单位，则点C的坐标是____________，点D的坐标是_________；

（3）若将平行四边形ABCD平移到第一象限后，点B的坐标是（a,b），则点C的坐标是________，点D的坐标是_______；

（4）若点M在平面直角坐标系内，则在上图的直线AB上，并且在第一、第二象限内是否存在点F，使以A、C、F、M为顶点的四边形为菱形？若存在，请直接写出F点的坐标；若不存在，请说明理由。

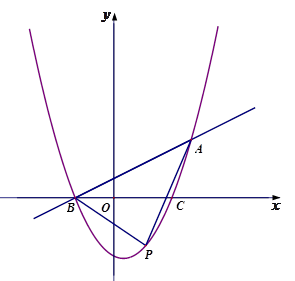
如图，二次函数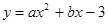的图象与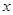轴交于B、C两点（点B在点C的左侧），一次函数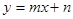的图象经过点B和二次函数图象上另一点A. 点A的坐标（4 ，3），.

（1）求二次函数和一次函数解析式；
（2）若点P在第四象限内，求面积S的最大值并求出此时点P的坐标；
（3）若点M在直线AB上，且与点A的距离是到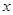轴距离的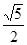倍，求点M的坐标.