
△ABC和△A′B′C′中,①AB=A′B′②BC=B′C′③AC=A′C′④∠A=∠A′,⑤∠B=∠B′⑥∠C=∠C′.则不能证出△ABC≌△A′B′C′的条件是( )
|
科目:初中数学 来源: 题型:
科目:初中数学 来源:不详 题型:单选题
| A.①②③ | B.①②⑤ | C.①②④ | D.②⑤⑥ |
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:
| 5 |
| 10 |
| 13 |
| 5 |
| 8 |
| 17 |
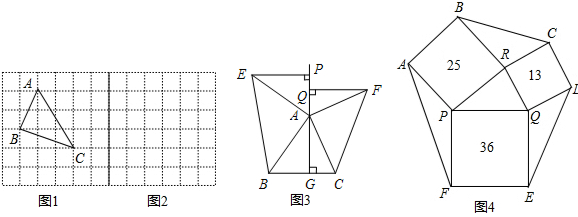
科目:初中数学 来源: 题型:阅读理解
| b |
| sinB |
| c |
| sinC |
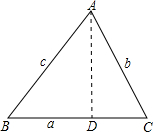 过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.| AD |
| AB |
| AD |
| AC |
| b |
| sinB |
| c |
| sinC |
| 6 |
科目:初中数学 来源: 题型:解答题
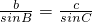
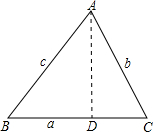 过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.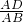 ,则AD=csinB
,则AD=csinB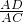 ,则AD=bsinC
,则AD=bsinC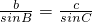
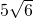 ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.科目:初中数学 来源:2009年江苏省连云港市中考数学原创试卷大赛(32)(解析版) 题型:解答题
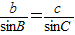
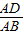 ,则AD=csinB
,则AD=csinB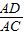 ,则AD=bsinC
,则AD=bsinC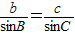
 ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.
科目:初中数学 来源:2009年江苏省连云港市中考数学原创试卷大赛(22)(解析版) 题型:解答题
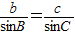
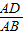 ,则AD=csinB
,则AD=csinB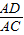 ,则AD=bsinC
,则AD=bsinC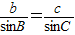
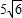 ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.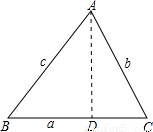
科目:初中数学 来源:2009年江苏省连云港市中考数学原创试卷大赛(1)(解析版) 题型:解答题
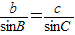
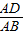 ,则AD=csinB
,则AD=csinB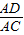 ,则AD=bsinC
,则AD=bsinC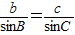
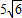 ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.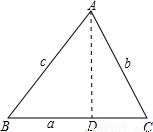
科目:初中数学 来源:广东省竞赛题 题型:单选题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com