计算：＋＋…＋＋(n为正整数)．

这个式子共有n项，属于异分母分数加减的类型．如果先通分，将各项化为同分母分数的话，分母将十分庞大，这是很困难的，在实际运算的时候也是不现实的，那么怎么办呢？

让我们分析一下各项的特点：都是的形式，当n取从1开始渐次增大的自然数时，就是各项了．可以把看成是各项的代表式．我们知道

－＝＝，

故＝－．

利用这一点，每一项都可以拆成两项，由于n是按自然数逐次递增的，所以前后两项拆开后会有相同部分可以抵消，如：

－

＝(－)＋(－)

＝1－＋－

＝．

所以可得

＋＋…＋＋

＝(－)＋(－)＋…＋(－)＋(－)

＝1－＋－＋…＋－＋－

＝1－

＝．

看！经过拆项以后，原本很复杂的计算，一下子简单了！诺长的一个式子，最后的结果也很简单．“巧拆”带来“巧算”．

利用这样拆分的方法，你想想下面的计算题，能否做到又快又准呢？

(1)＋＋…＋(n为大于2的整数)；

(2)＋＋…＋(n为正整数)；

(3)＋＋…＋(n为正整数)．

在你完成上面的计算后，可与同学们讨论一下，对于

＋＋…＋(n为正整数)

能否还采用这样的拆项方法进行巧算？为什么？再与同学们探索一下，对于下面的式子，如何计算？

＋＋＋…＋(n为正整数)．

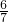一个分数的分子与分母都是正整数，且分子比分母小1，若分子和分母都减去1，则所得分数为小于的正数，则满足上述条件的分数共有

1. A.
   5个
2. B.
   6个
3. C.
   7个
4. D.
   8个