
等腰直角三角形的斜边长是有理数,则面积S是( )理数,周长l是( )理数.
|
科目:初中数学 来源:1995年第7届“五羊杯”初中数学竞赛初三试卷(解析版) 题型:选择题
科目:初中数学 来源: 题型:044
把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
(1)在上述旋转过程中,BH与CH有怎样的数量关系?四边形BHGK的面积有何变化?证明你发现的结论;
(2)连接HK,在上述旋转过程中,设BH=![]() ,△GKH的面积为
,△GKH的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)
在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的
科目:初中数学 来源:初中数学解题思路与方法 题型:044
把两个全等的等腰直角三角板ABC和EFG(其中直角边长约为4)叠放在一起(图1),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O按顺时针方向旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(图2).
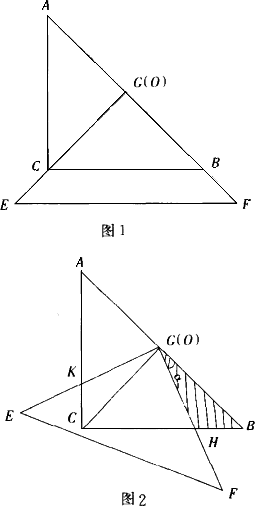
(1)在上述过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论;
(2)连结HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的![]() ?若存在,求出此时x的值,若不存在,说明理由.
?若存在,求出此时x的值,若不存在,说明理由.
科目:初中数学 来源:2013年四川省乐山市沙湾区九年级调研考试数学试卷(带解析) 题型:解答题
在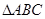 中,
中,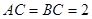 ,
,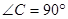 ,将一块等腰直角三角板的直角顶点放在斜边
,将一块等腰直角三角板的直角顶点放在斜边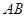 的中点
的中点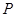 处,将三角板绕点
处,将三角板绕点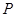 旋转,三角板的两直角边分别交射线
旋转,三角板的两直角边分别交射线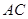 、
、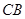 于
于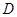 、
、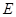 两点. 如图①、②、③是旋转三角板得到的图形中的三种情况,试探究:
两点. 如图①、②、③是旋转三角板得到的图形中的三种情况,试探究: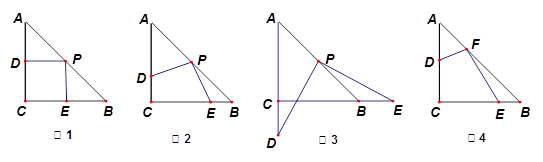
(1)三角板绕点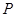 旋转,观察线段
旋转,观察线段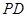 和
和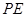 之间有什么数量关系?并结合图②加以证明;
之间有什么数量关系?并结合图②加以证明;
(2)三角板绕点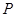 旋转,
旋转, 是否能成为等腰三角形?若能,写出所有
是否能成为等腰三角形?若能,写出所有 为等腰三角形时
为等腰三角形时 的长(直接写出答案即可);若不能,请说明理由;
的长(直接写出答案即可);若不能,请说明理由;
(3)如图 ,若将三角板的直角顶点放在斜边
,若将三角板的直角顶点放在斜边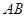 上的
上的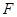 处,且
处,且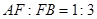 ,和前面一样操作,试问线段
,和前面一样操作,试问线段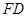 和
和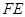 之间有什么数量关系?并结合图④证明你的结论.
之间有什么数量关系?并结合图④证明你的结论.
科目:初中数学 来源:2013年四川省乐山市沙湾区九年级调研考试数学试卷(解析版) 题型:解答题
在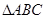 中,
中, ,
, ,将一块等腰直角三角板的直角顶点放在斜边
,将一块等腰直角三角板的直角顶点放在斜边 的中点
的中点 处,将三角板绕点
处,将三角板绕点 旋转,三角板的两直角边分别交射线
旋转,三角板的两直角边分别交射线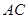 、
、 于
于 、
、 两点. 如图①、②、③是旋转三角板得到的图形中的三种情况,试探究:
两点. 如图①、②、③是旋转三角板得到的图形中的三种情况,试探究:

(1)三角板绕点 旋转,观察线段
旋转,观察线段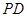 和
和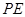 之间有什么数量关系?并结合图②加以证明;
之间有什么数量关系?并结合图②加以证明;
(2)三角板绕点 旋转,
旋转,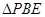 是否能成为等腰三角形?若能,写出所有
是否能成为等腰三角形?若能,写出所有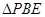 为等腰三角形时
为等腰三角形时 的长(直接写出答案即可);若不能,请说明理由;
的长(直接写出答案即可);若不能,请说明理由;
(3)如图 ,若将三角板的直角顶点放在斜边
,若将三角板的直角顶点放在斜边 上的
上的 处,且
处,且 ,和前面一样操作,试问线段
,和前面一样操作,试问线段 和
和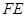 之间有什么数量关系?并结合图④证明你的结论.
之间有什么数量关系?并结合图④证明你的结论.
科目:初中数学 来源:不详 题型:解答题
 中,
中, ,
, ,将一块等腰直角三角板的直角顶点放在斜边
,将一块等腰直角三角板的直角顶点放在斜边 的中点
的中点 处,将三角板绕点
处,将三角板绕点 旋转,三角板的两直角边分别交射线
旋转,三角板的两直角边分别交射线 、
、 于
于 、
、 两点. 如图①、②、③是旋转三角板得到的图形中的三种情况,试探究:
两点. 如图①、②、③是旋转三角板得到的图形中的三种情况,试探究:
 旋转,观察线段
旋转,观察线段 和
和 之间有什么数量关系?并结合图②加以证明;
之间有什么数量关系?并结合图②加以证明; 旋转,
旋转, 是否能成为等腰三角形?若能,写出所有
是否能成为等腰三角形?若能,写出所有 为等腰三角形时
为等腰三角形时 的长(直接写出答案即可);若不能,请说明理由;
的长(直接写出答案即可);若不能,请说明理由; ,若将三角板的直角顶点放在斜边
,若将三角板的直角顶点放在斜边 上的
上的 处,且
处,且 ,和前面一样操作,试问线段
,和前面一样操作,试问线段 和
和 之间有什么数量关系?并结合图④证明你的结论.
之间有什么数量关系?并结合图④证明你的结论.科目:初中数学 来源:同步练习 数学九年级下册 题型:044
如图,把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,现将三角板EFG绕O点按顺时针方向旋转(旋转角α满足条件:![]() <α<
<α<![]() ),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
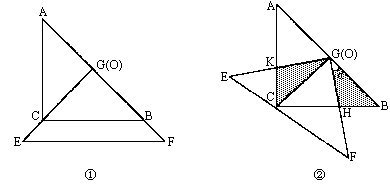
(1)在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论;
(2)连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的![]() ?若存在求出此时x的值;若不存在,说明理由.
?若存在求出此时x的值;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com