练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知：a＜0，b＞0，且|a|＞|b|，则|b+1|-|a-b|等于（　　）
    A．2b-a+1B．1+aC．a-1D．-1-a
    B
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源： 题型：

    15、已知：a＜0，b＞0，且|a|＞|b|，则|b+1|-|a-b|等于（　　）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    已知：a＜0，b＞0，且|a|＞|b|，则|b+1|-|a-b|等于（　　）
    A．2b-a+1B．1+aC．a-1D．-1-a

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：△ABC中，∠C＞∠B，AE平分∠BAC．
    （1）如图①AD⊥BC于D，若∠C=70°，∠B=30°，请你用量角器直接量出∠DAE的度数；
    （2）若△ABC中，∠B=α，∠C=β（α＜β），根据第一问的结果大胆猜想∠DAE与α、β间的等量关系，不必说理由；
    （3）如图②所示，在△ABC中AD⊥BC，AE平分∠BAC，F是AE上的任意一点，过F作FG⊥BC于G，且∠B=40°，∠C=80°，请你运用（2）中结论求出∠EFG的度数；
    （4）在（3）的条件下，若F点在AE的延长线上（如图③），其他条件不变，则∠EFG的度数大小发生改变吗？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    关于x的一元二次方程ax2+bx+c=0中，当b2-4a≥0，方程的两个根x1和x2不相等或相等，而且有x1+x2=-数学公式，x1•x2=数学公式；当b2-4ac＜0时，方程无实数解．比如方程x2-7x+12=0的两根x1=3，x2=4，则有b2-4ac=49-4×1×12=1＞0，而且x1+x2=7，x1•x2=12，2x2+x+1=0，b2-4ac=1-4×2×1=-7＜0，方程无解．根据以上情况解下列问题．
    已知Rt△ABC中，∠C=90°，BC=a，AC=b，a＞b，且a，b是关于x的方程x2-（m-1）x+（m+4）=0的两根，当AB=5时：（1）求m的值；（2）求a和b．

    查看答案和解析>>

    科目：初中数学 来源：2007-2008学年江苏省泰州市兴化市昭阳镇初中九年级（上）第一次月考数学试卷（解析版） 题型：解答题

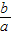    关于x的一元二次方程ax2+bx+c=0中，当b2-4a≥0，方程的两个根x1和x2不相等或相等，而且有x1+x2=-，x1•x2=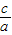；当b2-4ac＜0时，方程无实数解．比如方程x2-7x+12=0的两根x1=3，x2=4，则有b2-4ac=49-4×1×12=1＞0，而且x1+x2=7，x1•x2=12，2x2+x+1=0，b2-4ac=1-4×2×1=-7＜0，方程无解．根据以上情况解下列问题．
    已知Rt△ABC中，∠C=90°，BC=a，AC=b，a＞b，且a，b是关于x的方程x2-（m-1）x+（m+4）=0的两根，当AB=5时：（1）求m的值；（2）求a和b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列说法中： ①直线y=－2x＋4与直线y=x＋1的交点坐标是（1,1）；②一次函数＝kx+b，若k＞0，b＜0，那么它的图象过第一、二、三象限；③函数y＝－6x是一次函数，且y随着x的增大而减小；④已知一次函数的图象与直线y=－x＋1平行，且过点（8，2），那么此一次函数的解析式为y=－x＋6；⑤在平面直角坐标系中，函数的图象经过一、二、四象限⑥若一次函数中，y随x的增大而减小，则m的取值范围是m＞3学科网(Zxxk.Com)学⑦点A的坐标为(2，0)，点B在直线y=－x上运动，当线段AB最短时，点B的坐标为（－1,1）；⑧直线y=x―1与坐标轴交于A、B两点，点C在坐标轴上，△ABC为等腰三角形，则满足条件的点C最多有5个.      正确的有（   ）

    A．2个   B．3个     C．4个    D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    关于x的一元二次方程ax2+bx+c=0中，当b2-4a≥0，方程的两个根x1和x2不相等或相等，而且有x1+x2=-
    b
    a
    ，x1•x2=
    c
    a
    ；当b2-4ac＜0时，方程无实数解．比如方程x2-7x+12=0的两根x1=3，x2=4，则有b2-4ac=49-4×1×12=1＞0，而且x1+x2=7，x1•x2=12，2x2+x+1=0，b2-4ac=1-4×2×1=-7＜0，方程无解．根据以上情况解下列问题．
    已知Rt△ABC中，∠C=90°，BC=a，AC=b，a＞b，且a，b是关于x的方程x2-（m-1）x+（m+4）=0的两根，当AB=5时：（1）求m的值；（2）求a和b．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    关于x的一元二次方程ax2+bx+c=0中，当b2-4a≥0，方程的两个根x1和x2不相等或相等，而且有x1+x2=-
    b
    a
    ，x1•x2=
    c
    a
    ；当b2-4ac＜0时，方程无实数解．比如方程x2-7x+12=0的两根x1=3，x2=4，则有b2-4ac=49-4×1×12=1＞0，而且x1+x2=7，x1•x2=12，2x2+x+1=0，b2-4ac=1-4×2×1=-7＜0，方程无解．根据以上情况解下列问题．
    已知Rt△ABC中，∠C=90°，BC=a，AC=b，a＞b，且a，b是关于x的方程x2-（m-1）x+（m+4）=0的两根，当AB=5时：（1）求m的值；（2）求a和b．

    查看答案和解析>>

    科目：初中数学 来源：福建省中考真题 题型：解答题

    已知抛物线y=2x2，⊙O与抛物线交于A、B两点，AB两点所在的直线为l，⊙O的半径为2。
    （1）当x＞xB时，抛物线上存在一动点C，则随着C点的向上运动，三角形ABC面积不断增加，问三角形ABC面积每秒的增加量△S是什么？（友情提醒：C点的速度为v0·s-1）；
    （2）存在一点D在劣弧AB上运动（不与A、B重合）设D（h，k），问抛物线上是否存在点E使得三角形ABD与三角形ABE的面积相等？若存在，求出点E；若不存在，请说明理由；
    （3）F（m，n）（m＞0）是抛物线y=2x2上的点，OF⊥FG，G（a，0）（a＞m），△OFG的面积为S，且S=4n4，n是不大于40的整数，求OF2的最小值；
    （4）在抛物线上取两点J、K，xJ＜0，xk＞0，连接OJ、JK、OK，使得角OKJ=60°，再以OK、OJ、JK分别作等边三角形OKL、OJM、OKN，请你求出经过M、N、L三点的抛物线的解析式。

    查看答案和解析>>


    同步练习册答案