
科目:初中数学 来源:2011-2012学年重庆市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
重庆市某小企业为了节能,以行动支持创全国环保模范城市,从去年1至6月,该企业用水量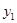 (吨)与月份x(
(吨)与月份x( ,且x取整数)之间的函数关系如下表:
,且x取整数)之间的函数关系如下表:
|
月份x(月) |
1 |
2 |
3 |
4 |
5 |
6 |
|
用水量 |
300 |
150 |
100 |
75 |
60 |
50 |
去年7至12月,用水量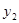 (吨)与月份x(
(吨)与月份x( ,且x取整数)的变化情况满足二次函数
,且x取整数)的变化情况满足二次函数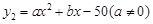 ,且去年7月和去年8月该企业的用水量都为62吨. (1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出
,且去年7月和去年8月该企业的用水量都为62吨. (1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出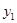 与x之间的函数关系式.并且直接写出
与x之间的函数关系式.并且直接写出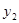 与x之间的函数关系式;
与x之间的函数关系式;
(2) 政府为了鼓励企业节约用水,决定对每月用水量不超过300吨的企业进行奖励. 去年1至6月奖励标准如下,以每月用水量300吨为标准,不足300吨的用水量每吨奖励资金 (元)与月份x满足函数关系式
(元)与月份x满足函数关系式 (
( ,且x取整数),如该企业去年3月用水量为100吨,那么该企业得到奖励资金为(
,且x取整数),如该企业去年3月用水量为100吨,那么该企业得到奖励资金为( )z元;去年7至12月奖励标准如下:以每月用水量300吨为标准,不足300吨的每吨奖励10元,如该企业去年7月份的用水量为62吨,那么该企业得到奖励资金为(
)z元;去年7至12月奖励标准如下:以每月用水量300吨为标准,不足300吨的每吨奖励10元,如该企业去年7月份的用水量为62吨,那么该企业得到奖励资金为(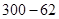 )×10元.请你求出去年哪个月政府奖励该企业的资金最多,并求出这个最多资金;
)×10元.请你求出去年哪个月政府奖励该企业的资金最多,并求出这个最多资金;
(3)在(2)问的基础上,今年1至6月,政府继续加大对节能企业的奖励,奖励标准如下:以每月用水量300吨为标准,不足300吨的部分每吨补助比去年12月每吨补助提高m%.在此影响下,该企业继续节水,1至3月每月的用水量都在去年3月份的基础上减少40吨.4至6月每月的用水量都在去年5月份的基础上减少m%,若政府今年1至6月奖励给该企业的资金为18000元,请你参考以下数据,估算出 m的整数值.(参考数据:
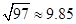
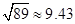
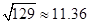 )
)
科目:初中数学 来源: 题型:解答题
 (9-1)、
(9-1)、 (9+1)与
(9+1)与 (25-1)、
(25-1)、 (25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;科目:初中数学 来源:2012年四川省内江市市中区中考数学模拟试卷(解析版) 题型:解答题
 (9-1)、
(9-1)、 (9+1)与
(9+1)与 (25-1)、
(25-1)、 (25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;科目:初中数学 来源:2004年全国中考数学试题汇编《三角形》(08)(解析版) 题型:解答题
 (9-1)、
(9-1)、 (9+1)与
(9+1)与 (25-1)、
(25-1)、 (25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;科目:初中数学 来源:2010年江苏省泰州市泰兴市五校联考中考数学模拟试卷(解析版) 题型:解答题
 (9-1)、
(9-1)、 (9+1)与
(9+1)与 (25-1)、
(25-1)、 (25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;科目:初中数学 来源:2009年江苏省中考数学模拟卷(2)(解析版) 题型:解答题
 (9-1)、
(9-1)、 (9+1)与
(9+1)与 (25-1)、
(25-1)、 (25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;科目:初中数学 来源:2009年江苏省常州市3月数学中考模拟卷(解析版) 题型:解答题
 (9-1)、
(9-1)、 (9+1)与
(9+1)与 (25-1)、
(25-1)、 (25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;科目:初中数学 来源:2009年安徽省淮南市潘集区九年级(下)第七次联考数学试卷(解析版) 题型:解答题
 (9-1)、
(9-1)、 (9+1)与
(9+1)与 (25-1)、
(25-1)、 (25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com