
科目:初中数学 来源: 题型:
 (2013•湖州一模)如图,平面直角坐标系xOy中,Rt△AOB的直角边OA在x轴的正半轴上,点B在第一象限,并且AB=3,OA=6,将△AOB绕点O逆时针旋转90度得到△COD.点P从点C出发(不含点C),沿射线DC方向运动,记过点D,P,B的抛物线的解析式为y=ax2+bx+c(a<0).
(2013•湖州一模)如图,平面直角坐标系xOy中,Rt△AOB的直角边OA在x轴的正半轴上,点B在第一象限,并且AB=3,OA=6,将△AOB绕点O逆时针旋转90度得到△COD.点P从点C出发(不含点C),沿射线DC方向运动,记过点D,P,B的抛物线的解析式为y=ax2+bx+c(a<0).科目:初中数学 来源: 题型:
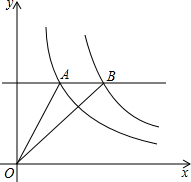 (2013•成都一模)如图,是反比例函数y=
(2013•成都一模)如图,是反比例函数y=| k1 |
| x |
| k2 |
| x |
科目:初中数学 来源: 题型:

科目:初中数学 来源: 题型:
| 3 | x |
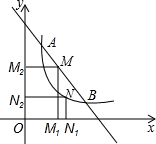 x的值;
x的值;科目:初中数学 来源:2008年全国中考数学试题汇编《三角形》(01)(解析版) 题型:选择题
 (k≠0)与△ABC有交点,则k的取值范围是( )
(k≠0)与△ABC有交点,则k的取值范围是( )
科目:初中数学 来源:2008年全国中考数学试题汇编《反比例函数》(01)(解析版) 题型:选择题
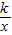 (k≠0)与△ABC有交点,则k的取值范围是( )
(k≠0)与△ABC有交点,则k的取值范围是( )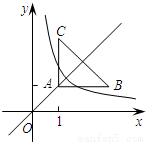
科目:初中数学 来源:2010年全国中考数学试题汇编《三角形》(01)(解析版) 题型:选择题
 (k≠0)与△ABC有交点,则k的取值范围是( )
(k≠0)与△ABC有交点,则k的取值范围是( )
科目:初中数学 来源:2010年全国中考数学试题汇编《反比例函数》(02)(解析版) 题型:选择题
 (k≠0)与△ABC有交点,则k的取值范围是( )
(k≠0)与△ABC有交点,则k的取值范围是( )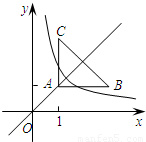
科目:初中数学 来源:2010年四川省攀枝花市中考数学试卷(解析版) 题型:选择题
 (k≠0)与△ABC有交点,则k的取值范围是( )
(k≠0)与△ABC有交点,则k的取值范围是( )
科目:初中数学 来源:2009年浙江省杭州市萧山区中考模拟数学试卷(闻堰镇中 杜国娟)(解析版) 题型:选择题
 (k≠0)与△ABC有交点,则k的取值范围是( )
(k≠0)与△ABC有交点,则k的取值范围是( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com