
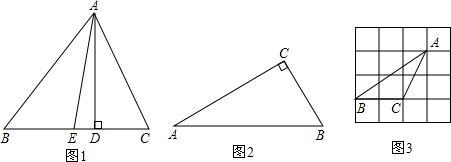
科目:初中数学 来源: 题型:
| DE | BE |
科目:初中数学 来源: 题型:解答题
 ,B=a-b
,B=a-b (a、b、m均为正有理数)都是无理数,若满足①A+B=2a为有理数;②AB=a2-mb2为有理数,则称A、B两数为姐妹数(如3+2
(a、b、m均为正有理数)都是无理数,若满足①A+B=2a为有理数;②AB=a2-mb2为有理数,则称A、B两数为姐妹数(如3+2 ,3-2
,3-2 ,∵3+2
,∵3+2 +3-2
+3-2 =6,(3+2
=6,(3+2 )(3-2
)(3-2 )=32-(2
)=32-(2 )2=9-8=1,∴6,1为有理数,则3
)2=9-8=1,∴6,1为有理数,则3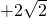 、3-2
、3-2 为姐妹数)
为姐妹数)科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:解答题
科目:初中数学 来源: 题型:
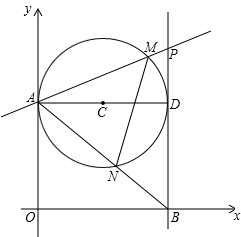 如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.
如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.| 32 | 25 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com