
若x2-x+M=(x-4)?N,则M、N分别为( )
|
科目:初中数学 来源: 题型:
| a-2y+1 |
| 2 |
| 1 |
| 2 |
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |
| 25 |
| 4 |
| 1 |
| 2 |
| (x2-x1)2+(y2-y1)2 |

科目:初中数学 来源: 题型:阅读理解
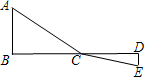 (2012•金牛区二模)阅读材料:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为
(2012•金牛区二模)阅读材料:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为| 16+(8-x)2 |
| 4+x2 |
| 8 |
| 3 |
| 25+(12-x)2 |
| 9+x2 |
| 13 |
| 13 |
科目:初中数学 来源: 题型:
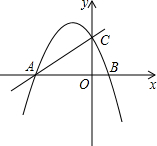 (2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-
(2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-| 1 |
| 2 |
| 25 |
| 4 |
| 1 |
| 2 |
| (x2-x1)2+(y2-y1)2 |
科目:初中数学 来源: 题型:
科目:初中数学 来源:2013-2014学年江苏苏州市九年级12月反馈测试数学试卷(解析版) 题型:填空题
记方程 的两实数根为x1、x2,在平面直角坐标系中有三点A、B、C,它们的坐标分别为A (x1,0),B(x2,0),C(0,12),若以此三点为顶点构成的三角形面积为6,则实数k的值为 .
的两实数根为x1、x2,在平面直角坐标系中有三点A、B、C,它们的坐标分别为A (x1,0),B(x2,0),C(0,12),若以此三点为顶点构成的三角形面积为6,则实数k的值为 .
科目:初中数学 来源: 题型:填空题
记方程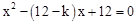 的两实数根为x1、x2,在平面直角坐标系中有三点A、B、C,它们的坐标分别为A (x1,0),B(x2,0),C(0,12),若以此三点为顶点构成的三角形面积为6,则实数k的值为 .
的两实数根为x1、x2,在平面直角坐标系中有三点A、B、C,它们的坐标分别为A (x1,0),B(x2,0),C(0,12),若以此三点为顶点构成的三角形面积为6,则实数k的值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com