
科目:初中数学 来源: 题型:
| 2 | 3 |
科目:初中数学 来源: 题型:
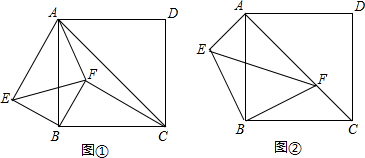
| 3 |
科目:初中数学 来源: 题型:
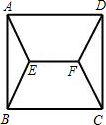 ABE=∠FDC=∠FCD=30°,∠AEF=∠DFE且AE=DF.
ABE=∠FDC=∠FCD=30°,∠AEF=∠DFE且AE=DF.科目:初中数学 来源: 题型:
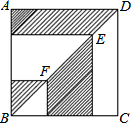 正方形ABCD边长为a,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图,则图中阴影部分的面积之和等于( )
正方形ABCD边长为a,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图,则图中阴影部分的面积之和等于( )| A、a2 | B、0.25a2 | C、0.5a2 | D、2 |
科目:初中数学 来源:2012-2013学年北京市第六十六中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
正方形ABCD中,点E、F为对角线BD上两点,DE=BF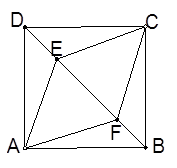
(1)四边形AECF是什么四边形? 为什么?
(2)若EF=4cm,DE=BF=2cm,求四边形AECF的周长。
科目:初中数学 来源:2010年江西省抚州市临川区罗湖中学数学中考模拟试卷(一)(解析版) 题型:解答题
 ?若存在,求出BP的长;若不存在,说明理由.
?若存在,求出BP的长;若不存在,说明理由.科目:初中数学 来源:2014届北京市八年级下学期期中考试数学试卷(解析版) 题型:解答题
正方形ABCD中,点E、F为对角线BD上两点,DE=BF

(1)四边形AECF是什么四边形? 为什么?
(2)若EF=4cm,DE=BF=2cm,求四边形AECF的周长。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com