科目：初中数学 来源： 题型：

查看答案和解析>>

科目：初中数学 来源：2012-2013年山东嘉祥萌山初级中学八年级上期中综合复习检测数学试卷（带解析） 题型：单选题

查看答案和解析>>

科目：初中数学 来源：2014届山东嘉祥萌山初级中学八年级上期中综合复习检测数学试卷（解析版） 题型：选择题

查看答案和解析>>

科目：初中数学 来源：不详 题型：单选题

查看答案和解析>>

科目：初中数学 来源： 题型：单选题

查看答案和解析>>

科目：初中数学 来源：解题升级解题快速反应一典通八年级数学 题型：044

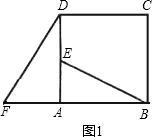
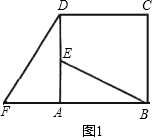
如图所示，正方形ABCD中，E是AD的中点，F是BA延长线上的一点，AF＝AB．(1)求证：△ABE≌△ADF．

(2)阅读下列材料：

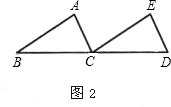
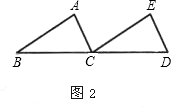
如图所示，把△ABC沿直线BC平行移动线段BC的长度，可以变到△ECD的位置；

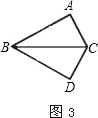
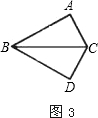
如图所示，以BC为轴把△ABC翻折，可以变到△DBC的位置；

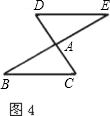
如图所示，以点A为中心，把△ABC旋转，可以变到△AED的位置．

像这样，其中一个三角形由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状大小的图形变换叫做三角形的全等变换．

回答下列问题：

①如图所示，可以通过平行移动、翻折、旋转中的哪一种方法，使△ABE变到△ADF的位置？答：________．

②指出图中线段BE与DF之间的关系．答：________．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图1，在正方形ABCD中，E是AD的中点，F是BA延长线上的一点，AF=

1

2

AB．（1）求证△ABE≌△ADF；

（2）阅读下列材料：
如图2，把△ABC沿直线BC平行移动线段BC的长度，可以变到△ECD的位置；

如图3，以BC为轴把△ABC翻折180°，可以变到△DBC的位置；

如图4，以点A为中心把△ABC旋转180°，可以变到△AED的位置．

像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状大小的图形变换，叫做三角形的全等变换．
（3）回答下列问题：
①在图1中，可以通过平行移动、翻折、旋转中的哪一种方法使△ABE变到△ADF的位置，
答：

 

．
②指出图1中，线段BE与DF之间的关系．
答：

 

．

查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

如图1，在正方形ABCD中，E是AD的中点，F是BA延长线上的一点，AF=

1

2

AB．（1）求证△ABE≌△ADF；



（2）阅读下列材料：
如图2，把△ABC沿直线BC平行移动线段BC的长度，可以变到△ECD的位置；



如图3，以BC为轴把△ABC翻折180°，可以变到△DBC的位置；



如图4，以点A为中心把△ABC旋转180°，可以变到△AED的位置．



像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状大小的图形变换，叫做三角形的全等变换．
（3）回答下列问题：
①在图1中，可以通过平行移动、翻折、旋转中的哪一种方法使△ABE变到△ADF的位置，
答：______．
②指出图1中，线段BE与DF之间的关系．
答：______．

查看答案和解析>>

科目：初中数学 来源：《23.2 中心对称》2010年同步练习4（解析版） 题型：解答题

如图1，在正方形ABCD中，E是AD的中点，F是BA延长线上的一点，AF=．（1）求证△ABE≌△ADF；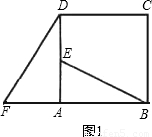

（2）阅读下列材料：
如图2，把△ABC沿直线BC平行移动线段BC的长度，可以变到△ECD的位置；

如图3，以BC为轴把△ABC翻折180°，可以变到△DBC的位置；

如图4，以点A为中心把△ABC旋转180°，可以变到△AED的位置．

像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状大小的图形变换，叫做三角形的全等变换．
（3）回答下列问题：
①在图1中，可以通过平行移动、翻折、旋转中的哪一种方法使△ABE变到△ADF的位置，
答：______．
②指出图1中，线段BE与DF之间的关系．
答：______．

查看答案和解析>>

科目：初中数学 来源：拱墅区一模 题型：单选题

如图，在△ABC中，已知∠C=90°，AC=BC=4，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持AE=CF，连接DE、DF、EF．在此运动变化的过程中，有下列结论：
①四边形CEDF有可能成为正方形；②△DFE是等腰直角三角形；③四边形CEDF的面积是定值；④点C到线段EF的最大距离为

2

．其中正确的结论是（　　）

A．①④

B．②③

C．①②④

D．①②③④

查看答案和解析>>